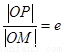题目内容
已知曲线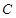 是动点
是动点 到两个定点
到两个定点 、
、 距离之比为
距离之比为 的点的轨迹。
的点的轨迹。
(1)求曲线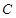 的方程;(2)求过点
的方程;(2)求过点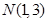 与曲线
与曲线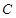 相切的直线方程。
相切的直线方程。
【答案】
(1)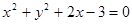 ;(2)
;(2)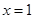 ,
,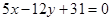 。
。
【解析】
试题分析:(1)在给定的坐标系里,设点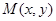 。
。
由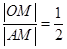 及两点间的距离公式,得
及两点间的距离公式,得 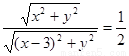 , ①…………3分
, ①…………3分
将①式两边平方整理得: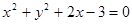
即所求曲线方程为: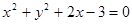 ②…………………………5分
②…………………………5分
(2)由(1)得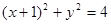 ,其圆心为
,其圆心为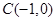 ,半径为
,半径为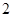 。
。
i)当过点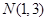 的直线的斜率不存在时,直线方程为
的直线的斜率不存在时,直线方程为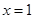 ,显然与圆相切;…6分
,显然与圆相切;…6分
ii) 当过点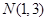 的直线的斜率存在时,设其方程为
的直线的斜率存在时,设其方程为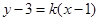
即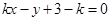 ……………7分
……………7分
由其与圆相切得圆心到该直线的距离等于半径,得
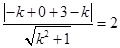 ,解得
,解得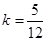 , …………8分
, …………8分
此时直线方程为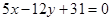 …………9分
…………9分
所以过点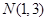 与曲线
与曲线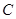 相切的直线方程为
相切的直线方程为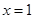 ,
,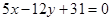 。………10分
。………10分
考点:两点间的距离公式;点到直线的距离公式;轨迹方程的求法;
点评:求轨迹方程的基本步骤:①建立适当的平面直角坐标系,设P(x,y)是轨迹上的任意一点;②寻找动点P(x,y)所满足的条件;③用坐标(x,y)表示条件,列出方程f(x,y)=0;④化简方程f(x,y)=0为最简形式;⑤证明所得方程即为所求的轨迹方程,注意验证。

练习册系列答案
相关题目
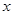 轴上,它的一个项点到两个焦点的距离分别是7和1
轴上,它的一个项点到两个焦点的距离分别是7和1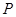 为椭圆C的动点,M为过P且垂直于
为椭圆C的动点,M为过P且垂直于