题目内容
等差数列{an}中,a1=25,S17=S9,问数列前多少项之和最大,并求出最大值.
解:解法一:∵a1=25,S17=S9,
∴17a1+ d=9a1+
d=9a1+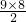 d,解得d=-2.
d,解得d=-2.
∴Sn=25n+ ×(-2)
×(-2)
=-n2+26n=-(n-13)2+169.
由二次函数的知识可知:当n=13时,
S13=169,即前13项之和最大,最大值为169.
解法二:同方法一:得d=-2,
∴an=25+(n-1)×(-2)=-2n+27,由an-1≤an≤an+1,
可解得 ≤n≤
≤n≤ ,又∵n∈N*,
,又∵n∈N*,
∴当n=13时,Sn取得最大值,最大值为169.
分析:解法一,由等差数列的求和公式可得17a1+ d=9a1+
d=9a1+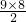 d,解之可得d=-2,进而可得Sn=-n2+26n,由二次函数的性质可得;解法二,求出公差后可得通项,由an-1≤an≤an+1可得n的范围,结合n为自然数可得结论.
d,解之可得d=-2,进而可得Sn=-n2+26n,由二次函数的性质可得;解法二,求出公差后可得通项,由an-1≤an≤an+1可得n的范围,结合n为自然数可得结论.
点评:本题考查等差数列的性质,涉及二次函数的性质,属中档题
∴17a1+
 d=9a1+
d=9a1+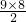 d,解得d=-2.
d,解得d=-2.∴Sn=25n+
 ×(-2)
×(-2)=-n2+26n=-(n-13)2+169.
由二次函数的知识可知:当n=13时,
S13=169,即前13项之和最大,最大值为169.
解法二:同方法一:得d=-2,
∴an=25+(n-1)×(-2)=-2n+27,由an-1≤an≤an+1,
可解得
 ≤n≤
≤n≤ ,又∵n∈N*,
,又∵n∈N*,∴当n=13时,Sn取得最大值,最大值为169.
分析:解法一,由等差数列的求和公式可得17a1+
 d=9a1+
d=9a1+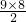 d,解之可得d=-2,进而可得Sn=-n2+26n,由二次函数的性质可得;解法二,求出公差后可得通项,由an-1≤an≤an+1可得n的范围,结合n为自然数可得结论.
d,解之可得d=-2,进而可得Sn=-n2+26n,由二次函数的性质可得;解法二,求出公差后可得通项,由an-1≤an≤an+1可得n的范围,结合n为自然数可得结论.点评:本题考查等差数列的性质,涉及二次函数的性质,属中档题

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目