题目内容
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2a n+1.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:对一切正整数n,有
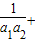
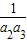 +…+
+…+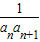 <
< .
.
【答案】分析:(Ⅰ)设等差数列{an}的公差为d,可得关于d和a1的方程组,解之代入通项公式可得;(Ⅱ)可得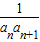 =
= (
(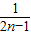 -
-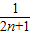 ),裂项相消可得
),裂项相消可得
原式= (1-
(1-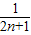 ),由放缩法可得答案.
),由放缩法可得答案.
解答:解:(Ⅰ)设等差数列{an}的公差为d,
则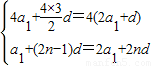 ,解得
,解得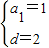
故数列{an}的通项公式为:an=2n-1,n∈N*.…(6分)
(Ⅱ)∵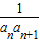 =
=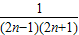 =
= (
(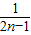 -
-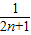 ),
),
∴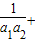
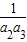 +…+
+…+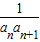
= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(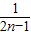 -
-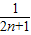 )]
)]
= (1-
(1-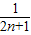 )<
)< .…(12分)
.…(12分)
点评:本题考查等差数列的通项公式和求和公式,涉及裂项相消法求数列的和,属中档题.
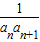 =
= (
(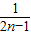 -
-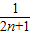 ),裂项相消可得
),裂项相消可得原式=
 (1-
(1-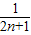 ),由放缩法可得答案.
),由放缩法可得答案.解答:解:(Ⅰ)设等差数列{an}的公差为d,
则
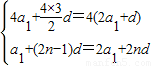 ,解得
,解得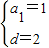
故数列{an}的通项公式为:an=2n-1,n∈N*.…(6分)
(Ⅱ)∵
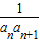 =
=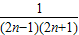 =
= (
(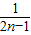 -
-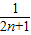 ),
),∴
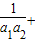
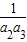 +…+
+…+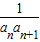
=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(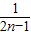 -
-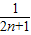 )]
)]=
 (1-
(1-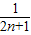 )<
)< .…(12分)
.…(12分)点评:本题考查等差数列的通项公式和求和公式,涉及裂项相消法求数列的和,属中档题.

练习册系列答案
相关题目