题目内容
动圆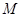 经过双曲线
经过双曲线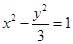 左焦点且与直线
左焦点且与直线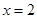 相切,则圆心
相切,则圆心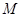 的轨迹方程是( )
的轨迹方程是( )
A. | B.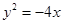 | C. | D.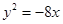 |
C
解析试题分析:双曲线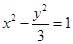 的焦点在x轴上且左焦点的坐标为
的焦点在x轴上且左焦点的坐标为 ,则圆心M满足到定点
,则圆心M满足到定点 与定直线
与定直线 的距离相等,故满足抛物线的定义,故动圆圆心M的轨迹是以点
的距离相等,故满足抛物线的定义,故动圆圆心M的轨迹是以点 为焦点的抛物线
为焦点的抛物线 ,故选C
,故选C
考点:抛物线定义 双曲线

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
如图,直线y=m与抛物线y2=4x交于点A,与圆(x-1)2+y2=4的实线部分交于点B,F为抛物线的焦点,则三角形ABF的周长的取值范围是 ( )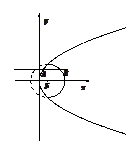
| A.(2,4) | B.(4,6) | C.[2,4] | D.[4,6] |
抛物线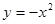 的焦点坐标为 ( )
的焦点坐标为 ( )
A.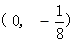 | B.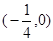 | C.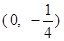 | D.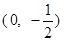 |
点 是椭圆上的一点,
是椭圆上的一点,  是焦点, 且, 则△
是焦点, 且, 则△ 的面积是
的面积是
A.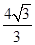 | B. | C. | D.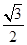 |
双曲线 -
- =1(a>0,b>0)的离心率为2,则
=1(a>0,b>0)的离心率为2,则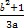 的最小值为( )
的最小值为( )
A.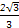 | B.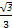 | C.2 | D.1 |
双曲线x2-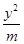 =1的离心率大于
=1的离心率大于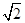 的充分必要条件是( )
的充分必要条件是( )
A.m>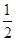 | B.m≥1 |
| C.m>1 | D.m>2 |
已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为( )
A. | B. |
| C.1 | D.2 |
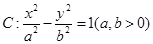 的左、右焦点分别为
的左、右焦点分别为
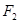 ,过
,过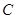 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为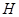 ,若
,若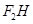 的中点
的中点 在双曲线
在双曲线
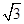
 =1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).
=1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).


