题目内容
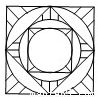
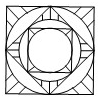 夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是
夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是(
)na
| ||
| 2 |
(
)na
.
| ||
| 2 |
分析:先根据正方形的对角线长为2a,求出正方形的边长为
a,即为第二正方形的对角线的长,从而求出第一个内切圆的半径,同理求出第二个内切圆的半径,然后归纳推理得到第n个内切圆的半径.
| 2 |
解答:解:∵正方形的对角线长为2a,
∴正方形的边长为
a,即为第二正方形的对角线的长
∵在正方形内作一个内切圆,则边长即为内切圆的直径
∴第一个内切圆的半径为
a
第一个内切圆的半径为
×
a=(
)2a
依此类推得作到第n个内切圆,它的半径是(
)na
故答案为:(
)na
∴正方形的边长为
| 2 |
∵在正方形内作一个内切圆,则边长即为内切圆的直径
∴第一个内切圆的半径为
| ||
| 2 |
第一个内切圆的半径为
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
依此类推得作到第n个内切圆,它的半径是(
| ||
| 2 |
故答案为:(
| ||
| 2 |
点评:本题主要考查了数列的应用,以及正方形的内切圆的半径的求解和归纳推理,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 野营活动中,学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架P-ABC(如图)进行野炊训练,将炊事锅看作一个点Q,用吊绳PQ将炊事锅吊起烧水(锅的大小忽略不计).已知PC=130cm,A、B两点间距离为
野营活动中,学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架P-ABC(如图)进行野炊训练,将炊事锅看作一个点Q,用吊绳PQ将炊事锅吊起烧水(锅的大小忽略不计).已知PC=130cm,A、B两点间距离为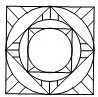 夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是________.
夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是________.