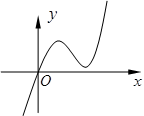题目内容
已知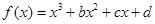 在区间[-1,2]上是减函数,那么
在区间[-1,2]上是减函数,那么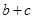 ( )
( )
A.有最大值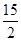 | B.有最大值-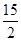 | C.有最小值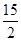 | D.有最小值-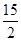 |
B
解析试题分析:因为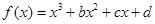 ,所以
,所以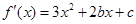 ,要使
,要使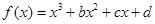 在区间[-1,2]上是减函数,需要
在区间[-1,2]上是减函数,需要 且
且 ,画出可行域,再画出目标函数
,画出可行域,再画出目标函数
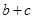 ,可以得出
,可以得出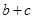 有最大值-
有最大值-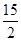 .
.
考点:本小题主要考查导函数与单调性的关系,及由线性规划知识求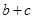 的取值范围.
的取值范围.
点评:要解决此类问题,需要掌握函数的导数与单调性的关系,此类题目中区间[-1,2]是减区间的子区间,而不一定是整个减区间,要看清题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若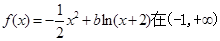 上是减函数,则
上是减函数,则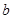 的取值范围是( )
的取值范围是( )
A. | B.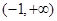 | C.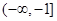 | D.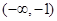 |
已知R上可导函数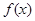 的图象如图所示,则不等式
的图象如图所示,则不等式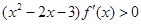 的解集为( )
的解集为( )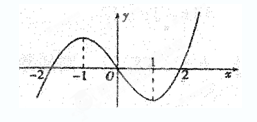
A. |
B.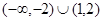 |
C.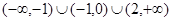 |
D.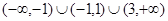 |
函数 的单调递增区间是 ( )
的单调递增区间是 ( )
A. | B.(0,3) | C.(1,4) | D.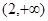 |
函数 有( )
有( )
| A.极大值5,极小值-27 | B.极大值5,极小值-11 |
| C.极大值5,无极小值 | D.极小值-27,无极大值 |
已知 既有极大值又有极小值,则
既有极大值又有极小值,则 的取值范围为( )
的取值范围为( )
A.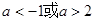 | B.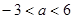 | C.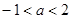 | D.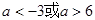 |
设定义在R上的函数 是最小正周期为
是最小正周期为 的偶函数,
的偶函数, 是
是 的导函数,当
的导函数,当 时,
时, ;当
;当 且
且 时 ,
时 , ,则函数
,则函数 在
在 上的零点个数为( )
上的零点个数为( )
| A.2 | B.4 | C.5 | D.8 |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,g(-2)=0且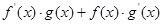 >0,则 不等式g (x)
>0,则 不等式g (x) f(x) <0的解集是( )
f(x) <0的解集是( )
| A.(-2, 0)∪(2,+ ∞) | B.(-2, 0)∪(0,2) |
| C.(-∞, -2)∪(2,+ ∞) | D.(-∞, -2)∪(0,2) |
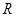 上的函数
上的函数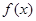 满足
满足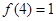 ,
,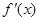 为
为 的图象如图所示.若两正数
的图象如图所示.若两正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )