题目内容
8.已知两不同的平面α,β和两条不重合的直线m,n有下列四个命题:①若m∥n,n⊥α则m⊥α.
②若m⊥α,m⊥β 则α∥β.
③若m⊥α,m∥n,n?β,则α⊥β.
④若m∥α,α∩β=n则m∥n.
其中真命题的有①②③.
分析 根据空间直线,平面间的位置关系的判定定理和性质定理,结合选项进行逐个判断即可.同时利用反例的应用
解答  解:对于①:若m∥n,n⊥α,根据线面垂直的性质得到m⊥α;故①为真命题;
解:对于①:若m∥n,n⊥α,根据线面垂直的性质得到m⊥α;故①为真命题;
对于②:若m⊥α,m⊥β,根据线面垂直的性质以及面面垂直的判定,得到α∥β;故②为真命题;
对于③:若m⊥α,m∥n,∴n⊥α,∵n?β,根据面面垂直的判定定理得到α⊥β,故③为真命题;
对于④:如图,若m∥α,α∩β=n,则m∥n不成立,故④为假命题;
故答案为:①②③.
点评 本题重点考查了空间中直线与直线平行、直线与平面平行、平面和平面平行、线面垂直、面面垂直的判定与性质等知识,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设等差数列{an}的公差为d.若数列{3${\;}^{{a}_{1}+{a}_{n}}$}为递减数列,则( )
| A. | a1d>0 | B. | a1d<0 | C. | d>0 | D. | d<0 |
13.下列程序的功能是( )
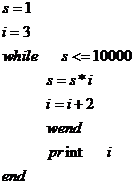
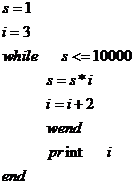
| A. | 求1×2×3×4×…×10 000的值 | |
| B. | 求2×4×6×8×…×10 000的值 | |
| C. | 求3×5×7×9×…×10 000的值 | |
| D. | 求满足1×3×5×…×n>10 000的最小正整数n |
20.复数$\frac{i-1}{i}$(i是虚数单位)在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |