题目内容
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足|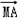 +
+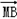 |=
|=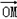 (
(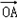 +
+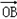 )+2。
)+2。
(1)求曲线C的方程;
(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l,问:是否存在定点P(0,t)(t<0),使得l与PA,PB都不相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值,若不存在,说明理由。
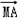 +
+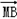 |=
|=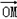 (
(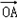 +
+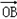 )+2。
)+2。(1)求曲线C的方程;
(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l,问:是否存在定点P(0,t)(t<0),使得l与PA,PB都不相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值,若不存在,说明理由。
解:(1)由 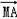 =(-2-x,1-y),
=(-2-x,1-y),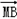 =(2-x,1-y)
=(2-x,1-y)
可得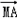 +
+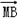 =(-2x,2-2y),
=(-2x,2-2y),
∴|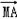 +
+ |=
|=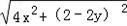 ,
,
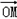 ·(
·(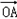 +
+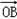 )+2=(x,y)(0,2)+2=2y+2
)+2=(x,y)(0,2)+2=2y+2
由题意可得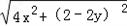 =2y+2,化简可得x2=4y.
=2y+2,化简可得x2=4y.
(2)假设存在点P(0,t)(t<0),满足条件,
则直线PA的方程是y=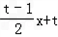 ,直线PB的方程是y=
,直线PB的方程是y=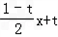
∵-2<x0<2,
∴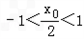
①当-1<t<0时,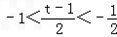 ,存在x0∈(-2,2),
,存在x0∈(-2,2),
使得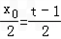
∴l∥PA,
∴当-1<t<0时,不符合题意;
②当t≤-1时,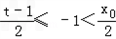 ,
,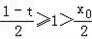 ,
,
∴l与直线PA,PB一定相交,分别联立方程组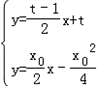 ,
,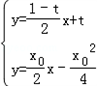 ,
,
解得D,E的横坐标分别是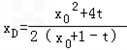 ,
,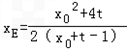
∴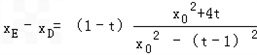
∵|FP|=-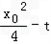
∴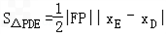 =
=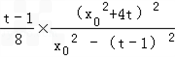
∴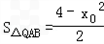
∴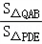 =
=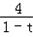 ×
×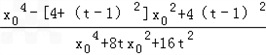
∵x0∈(-2,2),
△QAB与△PDE的面积之比是常数
∴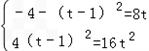 ,解得t=-1,
,解得t=-1,
∴△QAB与△PDE的面积之比是2。
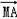 =(-2-x,1-y),
=(-2-x,1-y),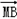 =(2-x,1-y)
=(2-x,1-y)可得
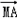 +
+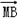 =(-2x,2-2y),
=(-2x,2-2y),∴|
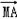 +
+ |=
|=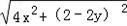 ,
,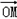 ·(
·(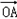 +
+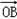 )+2=(x,y)(0,2)+2=2y+2
)+2=(x,y)(0,2)+2=2y+2由题意可得
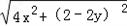 =2y+2,化简可得x2=4y.
=2y+2,化简可得x2=4y.(2)假设存在点P(0,t)(t<0),满足条件,
则直线PA的方程是y=
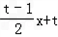 ,直线PB的方程是y=
,直线PB的方程是y=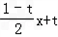
∵-2<x0<2,
∴
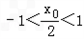
①当-1<t<0时,
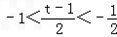 ,存在x0∈(-2,2),
,存在x0∈(-2,2),使得
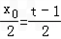
∴l∥PA,
∴当-1<t<0时,不符合题意;
②当t≤-1时,
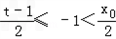 ,
,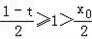 ,
,∴l与直线PA,PB一定相交,分别联立方程组
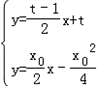 ,
,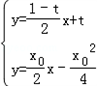 ,
,解得D,E的横坐标分别是
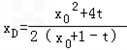 ,
,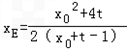
∴
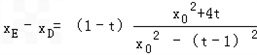
∵|FP|=-
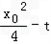
∴
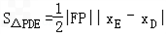 =
=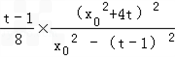
∴
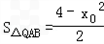
∴
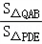 =
=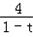 ×
×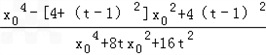
∵x0∈(-2,2),
△QAB与△PDE的面积之比是常数
∴
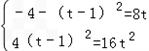 ,解得t=-1,
,解得t=-1,∴△QAB与△PDE的面积之比是2。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 |=
|=