题目内容
已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设
=
,
=
.
(Ⅰ)求
和
的夹角θ的余弦值;
(Ⅱ)若向量k
+
与k
-2
互相垂直,求实数k的值;
(Ⅲ)若向量λ
-
与
-λ
共线,求实数λ的值.
| a |
| AB |
| b |
| AC |
(Ⅰ)求
| a |
| b |
(Ⅱ)若向量k
| a |
| b |
| a |
| b |
(Ⅲ)若向量λ
| a |
| b |
| a |
| b |
分析:(I)利用向量夹角公式即可得出;
(II)利用向量垂直于数量积的关系即可得出;
(III)利用向量共线定理即可得出.
(II)利用向量垂直于数量积的关系即可得出;
(III)利用向量共线定理即可得出.
解答:解:
=
=(1,1,0),
=
=(-1,0,2).
(Ⅰ)cosθ=
=
=-
,
∴
和
的夹角θ的余弦值为-
.
(Ⅱ) k
+
=(k-1,k,2),k
-2
=(k+2,k,-4)
∵向量k
+
与k
-2
互相垂直,
∴(k
+
)•(k
-2
)=(k-1,k,2)•(k+2,k,-4)=(k-1)(k+2)+k2-8=2k2+k-10=0
∴k=-
,或k=2.
(Ⅲ) λ
-
=(λ+1,λ,-2),
-λ
=(1+λ,1,-2λ)
∵向量λ
-
与
-λ
共线,∴存在实数μ,使得λ
-
=μ(
-λ
)
即(λ+1,λ,-2)=μ(1+λ,1,-2λ)∴
∴λ=1,或λ=-1.
| a |
| AB |
| b |
| AC |
(Ⅰ)cosθ=
| ||||
|
|
| -1+0+0 | ||||
|
| ||
| 10 |
∴
| a |
| b |
| ||
| 10 |
(Ⅱ) k
| a |
| b |
| a |
| b |
∵向量k
| a |
| b |
| a |
| b |
∴(k
| a |
| b |
| a |
| b |
∴k=-
| 5 |
| 2 |
(Ⅲ) λ
| a |
| b |
| a |
| b |
∵向量λ
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
即(λ+1,λ,-2)=μ(1+λ,1,-2λ)∴
|
∴λ=1,或λ=-1.
点评:熟练掌握向量夹角公式、向量垂直于数量积的关系、向量共线定理等是解题的关键.

练习册系列答案
相关题目
 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量 ,求向量
,求向量 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;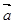 分别与向量
分别与向量 ,求向量
,求向量 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量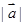 =
= ,求向量
,求向量