题目内容
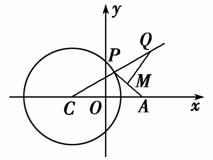
(2014·鹤壁淇县检测)如图所示,已知C为圆(x+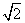 )2+y2=4的圆心,点A(
)2+y2=4的圆心,点A(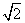 ,0),P是圆上的动点,点Q在圆的半径CP所在直线上,且
,0),P是圆上的动点,点Q在圆的半径CP所在直线上,且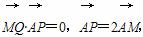 当点P在圆上运动时,求点Q的轨迹方程.
当点P在圆上运动时,求点Q的轨迹方程.

圆(x+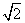 )2+y2=4的圆心为C(-
)2+y2=4的圆心为C(-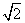 ,0),半径r=2,
,0),半径r=2,
∵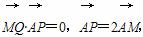 ∴MQ⊥AP,点M是AP的中点,即QM是AP的中垂线,连接AQ,则|AQ|=|QP|,∴||QC|-|QA||=||QC|-|QP||=|CP|=2,
∴MQ⊥AP,点M是AP的中点,即QM是AP的中垂线,连接AQ,则|AQ|=|QP|,∴||QC|-|QA||=||QC|-|QP||=|CP|=2,
又|AC|=2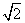 >2,根据双曲线的定义,点Q的轨迹是以C(-
>2,根据双曲线的定义,点Q的轨迹是以C(-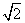 ,0),A(
,0),A(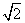 ,0)为焦点,实轴长为2的双曲线,由c=
,0)为焦点,实轴长为2的双曲线,由c=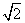 ,a=1,得b2=1,
,a=1,得b2=1,
因此点Q的轨迹方程为x2-y2=1.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
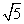 ,则它的渐近线方程为( )
,则它的渐近线方程为( )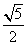 x
x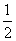 x D.y=±
x D.y=±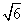 x
x x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________.
x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________. -1)=0表示的曲线是( )
-1)=0表示的曲线是( ) x和y=-
x和y=- ,P是AB的中点,则动点P的轨迹C的方程为________.
,P是AB的中点,则动点P的轨迹C的方程为________.

 B.4+
B.4+ D.
D.
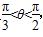 ,则其侧面展开图中心角α满足( )
,则其侧面展开图中心角α满足( )