题目内容
已知 ,
, ,且
,且 ∥
∥ .设函数y=f(x).
.设函数y=f(x).
(1)求函数y=f(x)的解析式.
(2)若在锐角△ABC中, ,边
,边 ,求△ABC周长的最大值.
,求△ABC周长的最大值.
解:(1)因为 ∥
∥ ,所以
,所以 ,
,
所以
(2)∵ ,
,
∴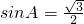 .∵
.∵ ,∴
,∴ .
.
又 ,
,
由余弦定理知,a2=b2+c2-2bccosA,3=(b+c)2-3bc
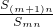 ,(b+c)2≤12,
,(b+c)2≤12,
∴ ,
, ,
,
∴△ABC周长的最大值为 .
.
分析:(1)根据 ∥
∥ ,直接可以得出
,直接可以得出 ,进而求出f(x)的解析式;
,进而求出f(x)的解析式;
(2)首先利用(1)得出 ,得出A的度数,然后利用余弦定理得出3=(b+c)2-3bc,利用均值不等式得出(b+c)2≤12,进而得出
,得出A的度数,然后利用余弦定理得出3=(b+c)2-3bc,利用均值不等式得出(b+c)2≤12,进而得出 ,即可求出周长的最大值.
,即可求出周长的最大值.
点评:本题考查了余弦定理、平行向量,(2)问得出∠A的度数是解题的关键,同时要灵活运用余弦定理.属于中档题.
 ∥
∥ ,所以
,所以 ,
,所以

(2)∵
 ,
,∴
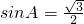 .∵
.∵ ,∴
,∴ .
. 又
 ,
,由余弦定理知,a2=b2+c2-2bccosA,3=(b+c)2-3bc
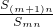 ,(b+c)2≤12,
,(b+c)2≤12,∴
 ,
, ,
,∴△ABC周长的最大值为
 .
.分析:(1)根据
 ∥
∥ ,直接可以得出
,直接可以得出 ,进而求出f(x)的解析式;
,进而求出f(x)的解析式;(2)首先利用(1)得出
 ,得出A的度数,然后利用余弦定理得出3=(b+c)2-3bc,利用均值不等式得出(b+c)2≤12,进而得出
,得出A的度数,然后利用余弦定理得出3=(b+c)2-3bc,利用均值不等式得出(b+c)2≤12,进而得出 ,即可求出周长的最大值.
,即可求出周长的最大值.点评:本题考查了余弦定理、平行向量,(2)问得出∠A的度数是解题的关键,同时要灵活运用余弦定理.属于中档题.

练习册系列答案
相关题目
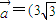 cosx,
cosx,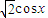 ),
),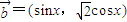 ,设函数f(x)=
,设函数f(x)=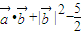 .
. ]时,求函数f(x)的值域;
]时,求函数f(x)的值域;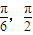 ]且f(α)=
]且f(α)=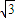 ,求f(
,求f(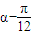 )的值.
)的值. ,其中ω>0.设函数
,其中ω>0.设函数 ,且函数f(x)的周期为π.
,且函数f(x)的周期为π.