题目内容
(12分)曲线C是中心在原点,焦点在![]() 轴上的双曲线,已知它的一个焦点F的坐标为(2,0),一条渐进线的方程为
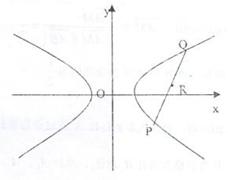
轴上的双曲线,已知它的一个焦点F的坐标为(2,0),一条渐进线的方程为![]() ,过焦点F作直线交曲线C的右支于P.Q两点,R是弦PQ的中点。
,过焦点F作直线交曲线C的右支于P.Q两点,R是弦PQ的中点。
![]() (Ⅰ)求曲线C的方程;
(Ⅰ)求曲线C的方程;
![]() (Ⅱ)当点P在曲线C右支上运动时,求点R到
(Ⅱ)当点P在曲线C右支上运动时,求点R到![]() 轴距离的最小值;
轴距离的最小值;
![]() (Ⅲ)若在
(Ⅲ)若在![]() 轴在左侧能作出直线
轴在左侧能作出直线![]() ,使以线段pQ为直径的圆与直线L相切,求m的取值范围。
,使以线段pQ为直径的圆与直线L相切,求m的取值范围。
解析:(Ⅰ)设所求双曲线C的方程为![]() -
-![]() =1,
=1,![]()
由题意得:
所以,所求曲线C的方程为![]() ……………3分
……………3分
(Ⅱ)若弦PQ所在直线斜率K存在,则设其方程为y=k (x-2)
由
设点P![]()
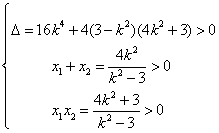
解得![]()
此时点R到y轴的距离![]()
而当弦PQ所在直线的斜率不存在时,点R到Y轴的距离为2,
所以,点R到Y轴距离的最小值为2。 ………………8分
(Ⅲ)因为直线L:x=m与以PQ为直径的圆相切
所以![]() 双曲线离心率e=
双曲线离心率e=![]() ,右准线方程为
,右准线方程为![]()
所以|PQ|=|PF|+|QF|=2 ![]()
所以![]() ,所以
,所以![]()

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目