题目内容
14.已知射手甲击中A目标的概率为0.9,射手乙击中A目标的概率为0.8,若甲、乙两人各向A目标射击一次,则射手甲或射手乙击中A目标的概率是0.98.分析 利用对立事件概率计算公式能求出甲、乙两人各向A目标射击一次,射手甲或射手乙击中A目标的概率.
解答 解:射手甲击中A目标的概率为0.9,射手乙击中A目标的概率为0.8,
甲、乙两人各向A目标射击一次,
射手甲或射手乙击中A目标的概率:
p=1-(1-0.9)(1-0.8)=0.98.
故答案为:0.98.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率计算公式、对立事件概率计算公式的合理运用.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5.已知集合A={x|y=lg(x+1)},B=$\left\{{\left.x\right|\frac{3-x}{x}<0}\right\}$,则有( )
| A. | -3∈A | B. | A∩B=(-1,0) | C. | A∪B=R | D. | A?B |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与椭圆$\frac{{x}^{2}}{{m}^{2}}$$+\frac{4{y}^{2}}{{m}^{2}}$=1的离心率互为倒数,则双曲线的渐近线方程是( )
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=$±\frac{\sqrt{3}}{2}$x |
3.已知函数f(x)=sinωx(ω>0)的最小正周期为π,则下列直线为f(x)的对称轴的是( )
| A. | x=$\frac{π}{2}$ | B. | x=$\frac{π}{3}$ | C. | x=$\frac{π}{4}$ | D. | x=$\frac{π}{5}$ |
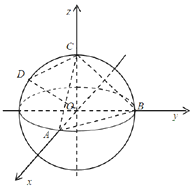 如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.
如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$. 在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,|OB|=3,点C是OB上靠近O点的三等分点,若$y=\frac{k}{x}(x>0)$函数的图象(图中未画出)与△OAB的边界至少有2个交点,则实数k的取值范围是$0≤k<\frac{{9\sqrt{2}}}{8}$.
在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,|OB|=3,点C是OB上靠近O点的三等分点,若$y=\frac{k}{x}(x>0)$函数的图象(图中未画出)与△OAB的边界至少有2个交点,则实数k的取值范围是$0≤k<\frac{{9\sqrt{2}}}{8}$.