题目内容
【题目】（本小题满分13分）
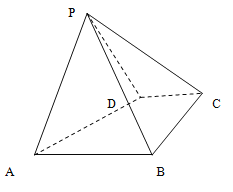
如图5，已知点
是圆心为
半径为1的半圆弧上从点
数起的第一个三等分点，
是直径，
，
平面
，点
是
的中点.
（1）求二面角
的余弦值.
（2）求点
到平面
的距离.
【答案】（1）
（2）
【解析】
试题分析：想求二面角的余弦值，得需要建立适当的坐标系，根据题中所给的条件，可以得出从一个起点出发的三条互相垂直的直线，符合建立坐标系的条件，求出相应的面的法向量，从而得出二面角的余弦值，对于第二问，可以通过三棱锥的体积相等来处理，也可以通过某个向量在法向量上的投影的问题来解决.
试题解析：
解 ：（1）∵
是圆心为
半径为1的半圆弧上
从点
数起的第一个三等分点，∴∠AOC=60，
∴
是等边三角形，
∴
. (1分)
∵C是圆周上的点，AB是直径，∴
，∴
(2分)
又
平面
，∴
两两垂直. 以点
为坐标原点，
、
、
分别为
、
、
轴的正向，建立空间直角坐标系，则
，
，
，
，
，
， （3分）
于是，
，
，
. (4分)
设
为平面
的法向量，
为平面
的法向量，
，
，取
得
. (5分)
，
，
取
得
. (6分)
， （7分）
因此，二面角
的余弦值是. (8分)
（2）方法一：由（1）知
（9分）
设
为平面
的法向量，则
，即
，取
得
. (10分)
设向量
和
所成的角为
，则
(12分)
设点
到平面
的距离为
，则
. (13分)
方法二：由（1）知
，
因为直线平面，所以，
，
，
于是，
，
.
因为
，点
是
的中点，所以
. （9分）
因此，
， (10分)
从而，
， (11分)
. (12分)
因为，
，设点到平面
的距离为
，则有
，即
，于是，
. (13分)
练习册系列答案
相关题目
