题目内容
已知函数f(x)=x2+bsinx-2,(b∈R),F(x)=f(x)+2,且对于任意实数x,恒有F(x-5)=F(5-x).(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调,求实数a的取值范围;
(3)函数h(x)=ln(1+x2)-
| 1 | 2 |
分析:(1)先表示出汗水F(x)的表达式,再根据F(x-5)=F(5-x)求出b的值,进而可确定函数f(x)的解析式.
(2)将(1)中求出的函数f(x)的解析式代入函数g(x)然后求导,将问题转化为g′(x)≥0或g′(x)≤0在(0,1)上恒成立.
(3)对函数h(x)进行求导,然后根据导函数的正负和原函数的单调性的关系判断函数的单调性,进而确定零点.
(2)将(1)中求出的函数f(x)的解析式代入函数g(x)然后求导,将问题转化为g′(x)≥0或g′(x)≤0在(0,1)上恒成立.
(3)对函数h(x)进行求导,然后根据导函数的正负和原函数的单调性的关系判断函数的单调性,进而确定零点.
解答:解:(1)由题设得:F(x)=x2+bsinx,
∵F(x-5)=F(5-x),
∴F(-x)=F(x)
∴x2-bsinx=x2+bsinx,
∴bsinx=0对于任意实数x都成立,
∴b=0
∴f(x)=x2-2.
(2)由g(x)=f(x)+2(x+1)+alnx=x2+2x+alnx,
得g′(x)=2x+2+
(x>0)
g(x)在(0,1)上恒单调,只需g′(x)≥0或g′(x)≤0在(0,1)上恒成立.
即2x2+2x+a≥0或2x2+2x+a≤0在(0,1)上恒成立.
∴a≥-(2x2+2x)或a≤-(2x2+2x)在(0,1)上恒成立.
设u(x)=-(2x2+2x),x∈(0,1),易知:u(x)∈(-4,0),
∴a≥0或a≤-4.
(3)令y=ln(1+x2)-
f(x),y′=
-x=-
,
令y′=0?x=0或x=1或x=-1,列表如下: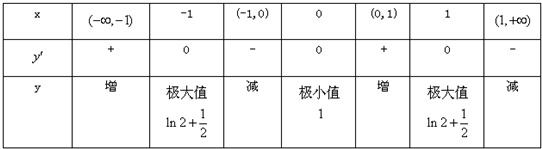
∴当k>ln2+
时,无零点;
当k<1或k=ln2+
时,有两个零点;
当k=1时,有三个零点;
当1<k<ln2+
时,有四个零点.
∵F(x-5)=F(5-x),
∴F(-x)=F(x)
∴x2-bsinx=x2+bsinx,
∴bsinx=0对于任意实数x都成立,
∴b=0
∴f(x)=x2-2.
(2)由g(x)=f(x)+2(x+1)+alnx=x2+2x+alnx,
得g′(x)=2x+2+
| a |
| x |
g(x)在(0,1)上恒单调,只需g′(x)≥0或g′(x)≤0在(0,1)上恒成立.
即2x2+2x+a≥0或2x2+2x+a≤0在(0,1)上恒成立.
∴a≥-(2x2+2x)或a≤-(2x2+2x)在(0,1)上恒成立.
设u(x)=-(2x2+2x),x∈(0,1),易知:u(x)∈(-4,0),
∴a≥0或a≤-4.
(3)令y=ln(1+x2)-
| 1 |
| 2 |
| 2x |
| 1+x2 |
| x(x+1)(x-1) |
| 1+x2 |
令y′=0?x=0或x=1或x=-1,列表如下:

∴当k>ln2+
| 1 |
| 2 |
当k<1或k=ln2+
| 1 |
| 2 |
当k=1时,有三个零点;
当1<k<ln2+
| 1 |
| 2 |
点评:本题主要考查函数的单调性、极值点与其导函数之间的关系.对原函数进行求导,然后列出函数f(x)、f'(x)随x变化的表格,其单调性、极值点即可呈现出来.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|