题目内容
在△ABC中,若cosAcosB=sin2
,则△ABC是( )
| C |
| 2 |
| A.等边三角形 | B.等腰三角形 | C.锐角三角形 | D.直角三角形 |
∵cosAcosB=sin2
=
,
又cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB,
∴2cosAcosB=1-cosC=1-(-cosAcosB+sinAsinB)=1+cosAcosB-sinAsinB,
移项合并得:cosAcosB+sinAsinB=1,即cos(A-B)=1,
又A和B都为三角形的内角,∴A-B=0,即A=B,
∴a=b,
则△ABC是等腰三角形.
故选B
| C |
| 2 |
| 1-cosC |
| 2 |
又cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB,
∴2cosAcosB=1-cosC=1-(-cosAcosB+sinAsinB)=1+cosAcosB-sinAsinB,
移项合并得:cosAcosB+sinAsinB=1,即cos(A-B)=1,
又A和B都为三角形的内角,∴A-B=0,即A=B,
∴a=b,
则△ABC是等腰三角形.
故选B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
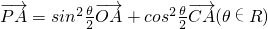 ,则
,则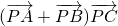 的最小值是________.
的最小值是________.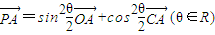 ,则
,则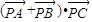 的最小值是 .
的最小值是 .