题目内容
椭圆的对称中心在坐标原点,一个顶点为![]() ,
,
右焦点![]() 与点
与点![]() 的距离为
的距离为![]() 。
。
(1)求椭圆的方程;
(2)是否存在斜率![]() 的直线
的直线![]() :
:![]() ,使直线
,使直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() 满足
满足![]() ,若存在,求直线
,若存在,求直线![]() 的倾斜角
的倾斜角![]() ;若不存在,说明理由。
;若不存在,说明理由。
【解】(1)依题意,设椭圆方程为![]() ,则其右焦点坐标为
,则其右焦点坐标为
![]() ,由
,由![]()
![]() ,得
,得![]() ,
,
即![]() ,解得
,解得![]() 。
。
又 ∵![]() ,∴
,∴ ![]() ,即椭圆方程为
,即椭圆方程为![]() 。 …………4分
。 …………4分
(2)由![]() 知点
知点![]() 在线段
在线段![]() 的垂直平分线上,
的垂直平分线上,
由 消去
消去![]() 得
得![]() 即
即![]() (*)
(*)
由![]() ,得方程(*)的
,得方程(*)的![]() ,
,
即方程(*)有两个不相等的实数根。
设![]() 、
、![]() ,线段
,线段![]() 的中点
的中点![]() ,
,
则![]() ,
,![]()
![]() ,
,
![]()
![]() ,即
,即![]()
![]() ,∴直线
,∴直线![]() 的斜率为
的斜率为 ,
,
由![]() ,得
,得![]() ,
,
∴ ![]() ,解得:
,解得:![]() ,即
,即![]() ,
,
又![]() ,故
,故 ![]() ,或
,或![]() ,
,
∴ 存在直线![]() 满足题意,其倾斜角
满足题意,其倾斜角![]() ,或
,或![]() 。………………12分
。………………12分

练习册系列答案
相关题目
 的距离为2.
的距离为2. ,若存在,求直线l的倾斜角α;若不存在,说明理由.
,若存在,求直线l的倾斜角α;若不存在,说明理由.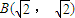 的距离为2.
的距离为2.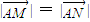 ,若存在,求直线l的倾斜角α;若不存在,说明理由.
,若存在,求直线l的倾斜角α;若不存在,说明理由.