题目内容
如图，在正方体ABCD-A1B1C1D1中，二面角C1-BD-C的正切值为 ．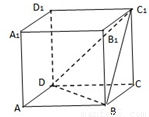
【答案】分析：取BD的中点O，连接OC1，OC，则∠COC1就是二面角C1-BD-C的平面角，由此能求出二面角C1-BD-C的正切值．
解答：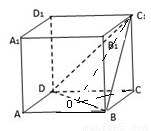
解：设正方体ABCD-A1B1C1D1的棱长为a，
则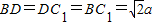
，CD=BC=CC1=a，
取BD的中点O，连接OC1，OC，则∠COC1就是二面角C1-BD-C的平面角，
∵CO=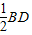
=
，
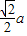∴tan∠COC1=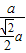
=
．
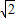故答案为：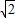
．
点评：本题考查二面角的正切值的求法，是基础题．解题时要认真审题，正方体性质的合理运用．
解答：
解：设正方体ABCD-A1B1C1D1的棱长为a，则
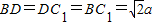，CD=BC=CC1=a，取BD的中点O，连接OC1，OC，则∠COC1就是二面角C1-BD-C的平面角，
∵CO=
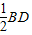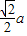=，∴tan∠COC1=
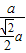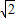=．故答案为：
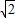．点评：本题考查二面角的正切值的求法，是基础题．解题时要认真审题，正方体性质的合理运用．
练习册系列答案
相关题目
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（ ）