题目内容

在锐角△ABC中，角A，B，C所对的边分别为a，b，c，若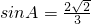 $数学公式$ ，a=2， $数学公式$ ，则b的值为________．

$\text{[math]}$
分析：题设条件中只给出 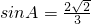$\text{[math]}$ ，a=2， $\text{[math]}$ ，欲求b的值，可由这些条件建立关于b的方程，根据所得方程进行研究，判断出解出其值的方法
解答：∵ $\text{[math]}$
∴ $\text{[math]}$ bcsinA= $\text{[math]}$ ，即 $\text{[math]}$ bc× $\text{[math]}$ = $\text{[math]}$ ，
∴bc=3 ①
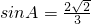又 $\text{[math]}$ ，a=2，锐角△ABC，可得cosA= $\text{[math]}$
由余弦定理得4=b²+c²-2bccosA=b²+c²-2×3× $\text{[math]}$ ，解得b²+c²=6 ②
由①②解得b=c，代入①得b=c= $\text{[math]}$
故答案为 $\text{[math]}$
点评：本题考查余弦定理，解题的关键是熟练掌握余弦定理与三角形的面积公式，解题过程中对所得出的数据进行分析也很重要，通过对解出的数据进行分析判明转化的方向，本题考查了分析判断的能力，是一道能力型题，探究型题

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

己知在锐角△ABC中，角A，B，C所对的边分别为a，b，c，且tanC=

（Ⅰ）求角C大小；
（Ⅱ）当c=1时，求a²+b²的取值范围．

（2012•张掖模拟）在锐角△ABC中，角A、B、C所对的边分别为a、b、c．且

．
（1）求角A的大小及角B的取值范围；
（2）若a=

，求b²+c²的取值范围．

=(cosx+f(x)，sin(

．
（1）求函数f（x）的表达式，并指出f（x）的单调递减区间；
（2）在锐角△ABC中，角A、B、C所对的边分别为a，b，c，且f(A)=-

，bc=8，求△ABC的面积S．

在锐角△ABC中，角A，B，C所对的边分别为a，b，c．已知b²=ac且sinAsinC=

．
（Ⅰ）求角B的大小．
（Ⅱ）求函数f（x）=sin（x-B）+sinx（0≤x＜π）的最大值和最小值．

在锐角△ABC中，角A，B，C所对的边分别为a，b，c．已知cos2C=-

．
（Ⅰ）求sinC；
（Ⅱ）当c=2a，且b=3

时，求a及△ABC的面积．