题目内容
已知函数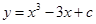 的图像与
的图像与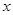 轴恰有两个公共点,则
轴恰有两个公共点,则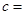
A.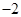 或2 B.
或2 B.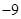 或3 C.
或3 C.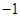 或1 D.
或1 D.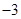 或1
或1
【答案】
A
【解析】
试题分析:求导函数可得y′=3(x+1)(x-1),令y′>0,可得x>1或x<-1;令y′<0,可得-1<x<1;
所以函数在(-∞,-1),(1,+∞)上单调增,(-1,1)上单调减,
所以函数在x=-1处取得极大值,在x=1处取得极小值。
因为函数y=x3-3x+c的图象与x轴恰有两个公共点,
所以极大值等于0或极小值等于0,所以1-3+c=0或-1+3+c=0,所以c=-2或2。
考点:利用导数来研究函数的极值;函数的零点与方程根的关系。
点评:本题考查导数知识的运用以及函数的单调性与极值。解题的关键是把问题转化为利用极大值等于0或极小值等于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
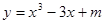 的图像与
的图像与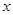 轴恰有两个公共点,则
轴恰有两个公共点,则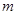 等于( )
等于( ) 的图像与x轴恰有两个公共点,则c=
的图像与x轴恰有两个公共点,则c=