题目内容
若角α的终边经过点P(1,-2),则cos2α-2sinαcosα的值为
1
1
.分析:由角α的终边经过点P(1,-2),利用任意角的三角函数定义求出sinα与cosα的值,代入原式计算即可求出值.
解答:解:∵角α的终边经过点P(1,-2),
∴sinα=-
,cosα=
,
则原式=
-2×(-
)×
=
+
=1.
故答案为:1
∴sinα=-
| 2 | ||
|
| 1 | ||
|
则原式=
| 1 |
| 5 |
| 2 | ||
|
| 1 | ||
|
| 1 |
| 5 |
| 4 |
| 5 |
故答案为:1
点评:此题考查了同角三角函数间的基本关系,以及任意角的三角函数定义,熟练掌握基本关系是解本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
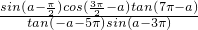 .
. .
. .
.