题目内容
已知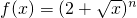 ,其中n∈N*.
,其中n∈N*.
(1)若展开式中含x3项的系数为14,求n的值;
(2)当x=3时,求证:f(x)必可表示成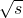
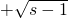 (s∈N*)的形式.
(s∈N*)的形式.
解:(1)由二项式定理可知,二项展开式的通项公式为 Tr+1= •2n-r•
•2n-r•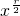 ,
,
令 =3,解得r=6,展开式中含x3项的系数为
=3,解得r=6,展开式中含x3项的系数为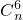 •2n-6=14,解得 n=7.
•2n-6=14,解得 n=7.
(2)当x=3时,f(x)=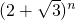 =
= •2n•
•2n• +
+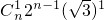 +
+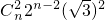
+…+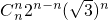 .
.
设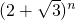 =x+
=x+ y=
y= +
+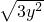 ,由于
,由于 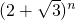 =
= ,a、b∈N*,
,a、b∈N*,
则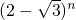 =
=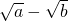 . …(7分)
. …(7分)
∵( )(
)(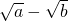 )=
)=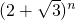 •
•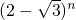 =1,
=1,
∴令 a=s,s∈N*,则必有 b=s-1,…(9分)
∴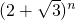 必可表示成
必可表示成 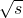
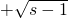 的形式,其中 s∈N*. …(10分)
的形式,其中 s∈N*. …(10分)
分析:(1)在二项展开式的通项公式中,令x的幂指数等于3,求得r的值,即可求得含x3的项,再根据展开式中含x3项的系数为14,求n的值.
(2)当x=3时,求得f(x)的解析式,由于若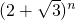 =
= ,a、b∈N*,则
,a、b∈N*,则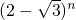 =
=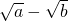 .再由 (
.再由 ( )(
)(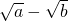 )=1,令 a=s,s∈N*,则必有 b=s-1,从而证得结论.
)=1,令 a=s,s∈N*,则必有 b=s-1,从而证得结论.
点评:本题二项式定理的应用,求展开式中某项的系数,属于中档题.
 •2n-r•
•2n-r•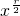 ,
,令
 =3,解得r=6,展开式中含x3项的系数为
=3,解得r=6,展开式中含x3项的系数为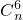 •2n-6=14,解得 n=7.
•2n-6=14,解得 n=7.(2)当x=3时,f(x)=
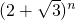 =
= •2n•
•2n• +
+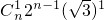 +
+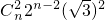
+…+
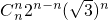 .
.设
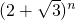 =x+
=x+ y=
y= +
+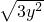 ,由于
,由于 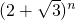 =
= ,a、b∈N*,
,a、b∈N*,则
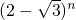 =
=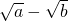 . …(7分)
. …(7分)∵(
 )(
)(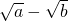 )=
)=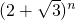 •
•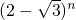 =1,
=1,∴令 a=s,s∈N*,则必有 b=s-1,…(9分)
∴
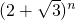 必可表示成
必可表示成 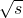
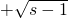 的形式,其中 s∈N*. …(10分)
的形式,其中 s∈N*. …(10分)分析:(1)在二项展开式的通项公式中,令x的幂指数等于3,求得r的值,即可求得含x3的项,再根据展开式中含x3项的系数为14,求n的值.
(2)当x=3时,求得f(x)的解析式,由于若
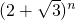 =
= ,a、b∈N*,则
,a、b∈N*,则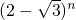 =
=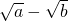 .再由 (
.再由 ( )(
)(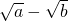 )=1,令 a=s,s∈N*,则必有 b=s-1,从而证得结论.
)=1,令 a=s,s∈N*,则必有 b=s-1,从而证得结论.点评:本题二项式定理的应用,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
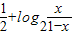 图象上任意两点,且
图象上任意两点,且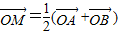 ,已知点M的横坐标为
,已知点M的横坐标为 .
.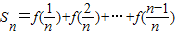 ,其中n∈N*且n≥2,
,其中n∈N*且n≥2,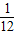 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.