Question

设函数f(x)=ax²+8x+3(a＜0),对于给定的负数a，有一个最大的正数l(a),使得在整个区间［0,l(a)］上，不等式|f(x)|≤5都成立.问a为何值时,l(a)最大？求出这个最大的l(a),证明你的结论.

Answer 1

分析：要使|f(x)|≤5在［0，l(a)］上都成立，只需|f(x)|在［0,l(a)］上的最大值不大于5即可.求|f(x)|在［0,l(a)］上的最大值，需判断-是否在［0，l(a)］内，故需分类讨论.                           

解：f(x)=a(x+)²+3-,

∵a＜0,∴f(x)_max=3-.

    当3-＞5,即-8＜a＜0时，

0＜l(a)＜-(如图(1)).

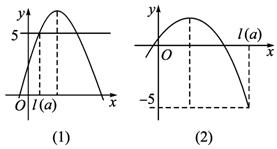
∴l(a)是方程ax²+8x+3=5的较小根,

l(a)==＜=.

    当3-≤5,即a≤-8时，l(a)＞-(如图(2)).

∴l(a)是方程ax²+8x+3=-5的较大根,

l(a)=≤，

    当且仅当a=-8时等号成立.

    由于＞,

    因此，当且仅当a=-8时，

l(a)取最大值.