题目内容

设f（x）=sin2x，则f′(
π
3
)=（　　）
分析：直接利用简单的复合函数的求导运算求出f′（x），然后将x=
π
3
代入，即可．
解答：解：因为f（x）=sin2x，所以f′（x）=（2x）′cos2x=2cos2x．
则f′(
π
3
)=2cos（2×
π
3
）=-1．
故选D．
点评：本题考查了简单的复合函数的导数，解答此题的关键是不要忘记对内层函数进行求导，是基础题．
练习册系列答案
相关题目
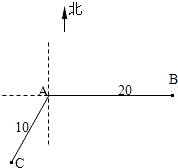精英家教网如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30°，相距10海里C处的乙船．
（Ⅰ）求处于C处的乙船和遇险渔船间的距离；
（Ⅱ）设乙船沿直线CB方向前往B处救援，其方向与
CA
成θ角，求f（x）=sin2θsinx+cos2θcosx（x∈R）的值域．
设φ∈(0，
π
4
)，函数f（x）=sin2（x+φ），且f(
π
4
)=
3
4
．
（Ⅰ）求φ的值；
（Ⅱ）若x∈[0，
π
2
]，求f（x）的最大值及相应的x值．
（2012•湖北）设函数f（x）=sin2ωx+2
3
sinωx•cosωx-cos2ωx+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
1
2
，1）．
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点(
π
4
，0)，求函数f（x）的值域．
（2012•许昌一模）设函数f（x）=sin2（x+
π
4
）-cos2（x+
π
4
）（x∈R），则函数f（x）是（　　）
设|φ|＜
π
4
，函数f（x）=sin2（x+φ）．若f（
π
4
）=
3
4
，则φ等于（　　）
A、-
π
12
B、-
π
6
C、
π
12
D、
π
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网