题目内容
(本小题共13分)
如图所示,正方形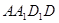 与矩形
与矩形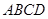 所在平面互相垂直,
所在平面互相垂直,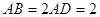 ,点E为
,点E为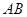 的中点。
的中点。

(Ⅰ)求证:
(Ⅱ) 求证: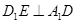
(Ⅲ)在线段AB上是否存在点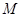 ,使二面角
,使二面角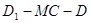 的大小为
的大小为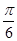 ?若存在,求出
?若存在,求出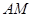 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
【答案】
(1)根据三角形的中位线,那么可以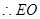 //
//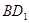 ,然后结合线面平行的判定定理可知结论。
,然后结合线面平行的判定定理可知结论。
(2)结合已知中正方形的心智,以及 ,结合线面垂直的性质定理得到线线垂直。
,结合线面垂直的性质定理得到线线垂直。
(3)
【解析】
试题分析:(Ⅰ) ,
点E为
,
点E为 的中点,连接
的中点,连接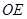 。
。
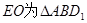 的中位线
的中位线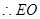 //
//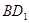 ……2分
……2分
又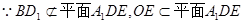
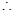
 ……4分
……4分
(II)
正方形 中,
中,
由已知可得: ,
, …….6分
…….6分
 ,
, …….7分
…….7分
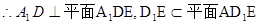
 …….8分
…….8分
(Ⅲ)由题意可得: ,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则
,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则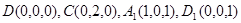 ,
,
 9分
9分
设
 10分
10分
设平面 的法向量为
的法向量为
则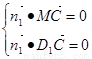
得 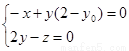 11分
11分
取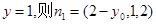 是平面
是平面 的一个法向量,而平面
的一个法向量,而平面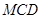 的一个法向量为
的一个法向量为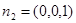 12分
12分
要使二面角 的大小为
的大小为
而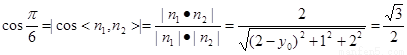
解得:
当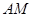 =
= 时,二面角
时,二面角 的大小为
的大小为
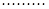 13分
13分
考点:空间中的线面平行和线线垂直以及二面角的求解
点评:解决平行和垂直的证明,一般要用到判定定理和性质定理,然后结合空间向量法来求解二面角,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 在
在 处取得极值,求a的值;
处取得极值,求a的值; 在
在 上的最大值.
上的最大值. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边 ,求
,求
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.