题目内容
如图1-2-12,四边形ABCD中,AC、BD交于O,过O作AB的平行线,与AD、BC分别交于E、F,与CD的延长线交于K,求证:KO2=KE·KF.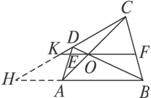
图1-2-12
思路分析:KO、KE、KF在一条直线上,要证明KO2=KE·KF,即要证![]() ,显然要寻找中间比,现有图形无法将线段KO、KE、KF与平行线分线段成比例定理及其推论联系起来,若延长CK、BA,设它们交于H,则图形中出现如上题所说的两个基本图形,这就不难将
,显然要寻找中间比,现有图形无法将线段KO、KE、KF与平行线分线段成比例定理及其推论联系起来,若延长CK、BA,设它们交于H,则图形中出现如上题所说的两个基本图形,这就不难将![]() 进行转换而找到中间比.
进行转换而找到中间比.
证明:延长CK、BA,设它们交于H,
∵KO∥HB,∴![]() .∴
.∴![]() ,即
,即![]() .
.
∵KF∥HB,同理可得![]() .∴
.∴![]() ,即KO2=KE·KF.
,即KO2=KE·KF.
深化升华 本题所作的辅助线,不仅构造了两个常见的基本图形,而且可以直接利用三角形一边的平行线的性质定理,找到![]() 与
与![]() 的中间比,使问题得以突破,也可以由两个基本图形直接得到
的中间比,使问题得以突破,也可以由两个基本图形直接得到![]() .
.

练习册系列答案
相关题目

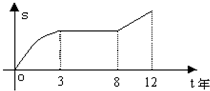 某工厂12年来某产品总产量S与时间t(年)的函数关系如图所示,下列四种说法:
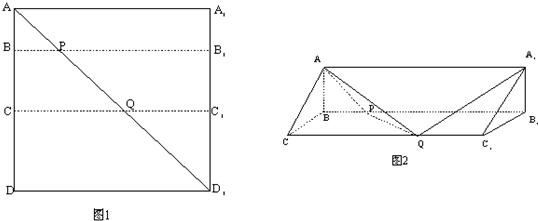
某工厂12年来某产品总产量S与时间t(年)的函数关系如图所示,下列四种说法: 如图,第n个图形是由正n+2边形“拓展”而来的.如图(1),在正三角形的每条边上,向外再“拓展”一个正三角形,得到一个有12个顶点的图形;如图(2),在正方形的四条边上向外“拓展”一个正方形,得到一个有20个顶点的图形,…,那么第n-2个图形中,共有
如图,第n个图形是由正n+2边形“拓展”而来的.如图(1),在正三角形的每条边上,向外再“拓展”一个正三角形,得到一个有12个顶点的图形;如图(2),在正方形的四条边上向外“拓展”一个正方形,得到一个有20个顶点的图形,…,那么第n-2个图形中,共有