题目内容
若y=a-bsinx(b>0)的最大值为
,最小值为-
,求函数y=asinx+b(x∈[-
,
π])的最值.
| 3 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 4 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由已知中y=a-bsinx(b>0)的最大值为
,最小值为-
,可求出a,b的值,进而根据正弦型函数的单调性,可得函数y=sinx+
在[-
,
π]上的最值.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 4 |
解答:
解:∵y=a-bsinx(b>0)的最大值为
,最小值为-
,
∴a=
=1,b=
=
,
即a=1,b=
.
则函数y=asinx+b可化为:y=sinx+
,(x∈[-
,
π])
∵函数y=sinx+
在[-
,
]上为增函数,在[
,
π]为减函数,
∴当x=
时,函数最大值为
,当x=-
时,最小值为0.
| 3 |
| 2 |
| 1 |
| 2 |
∴a=
| ||||
| 2 |
| ||||
| 2 |
| 1 |
| 2 |
即a=1,b=
| 1 |
| 2 |
则函数y=asinx+b可化为:y=sinx+
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 4 |
∵函数y=sinx+
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| 3 |
| 4 |
∴当x=
| π |
| 2 |
| 3 |
| 2 |
| π |
| 6 |
点评:本题考查的知识点是正弦函数的图象和性质,熟练掌握正弦函数最值与系数的关系,是解答的关键.

练习册系列答案
相关题目
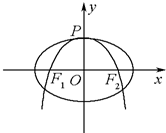 如图,抛物线C:y=-
如图,抛物线C:y=-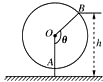 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h. 已知a、b、c为集合A={1,2,3,4,5}中三个不同的数,如框图给出的一个算法运行后输出一个整数a,则输出的数a=4的概率是
已知a、b、c为集合A={1,2,3,4,5}中三个不同的数,如框图给出的一个算法运行后输出一个整数a,则输出的数a=4的概率是