题目内容
销售甲,乙两种商品所得利润分别为P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式P=
t,Q=
.今将3万元资金投入经营甲,乙两种商品,其中对甲种商品投资x万元
(1)试建立总利润y(万元)关于x的函数表达式
(2)求x为多少时,总利润y最大?并写出最大利润.
| 1 |
| 5 |
| 3 |
| 5 |
| t |
(1)试建立总利润y(万元)关于x的函数表达式
(2)求x为多少时,总利润y最大?并写出最大利润.
分析:(1)通过设出甲投资以及乙投资的数目,设立函数表达式,根据函数式直接写出定义域.
(2)首先要对(1)的函数分析,设
=m,然后根据一元二次方程的求最值方法求解.
(2)首先要对(1)的函数分析,设
| 3-x |
解答:解:(1)因为对甲种商品投资x万元,
所以对乙种商品投资为3-x万元
由题意知:y=P+Q=
x+
(0≤x≤3)
(2)设
=m,
则m≥0且x=3-m2y=
x+
=
(3-m2)+
m
=-
(m2-3m-3)=-
(m-
)2+
所以当m=
即:
=
,
也就是x=
万元时,
总利润最大,ymax=
万元
故:应甲种商品投资
万元,对乙种商品投资
万元时,
总利润最大,最大值为
万元.
所以对乙种商品投资为3-x万元
由题意知:y=P+Q=
| 1 |
| 5 |
| 3 |
| 5 |
| 3-x |
(2)设
| 3-x |
则m≥0且x=3-m2y=
| 1 |
| 5 |
| 3 |
| 5 |
| 3-x |
| 1 |
| 5 |
| 3 |
| 5 |
=-
| 1 |
| 5 |
| 1 |
| 5 |
| 3 |
| 2 |
| 21 |
| 20 |
所以当m=
| 3 |
| 2 |
即:
| 3-x |
| 3 |
| 2 |
也就是x=
| 3 |
| 4 |
总利润最大,ymax=
| 21 |
| 20 |
故:应甲种商品投资
| 3 |
| 4 |
| 9 |
| 4 |
总利润最大,最大值为
| 21 |
| 20 |
点评:本题考查函数模型的选择与应用,通过对实际问题的分析,构造数学模型从而解决问题.需要对知识熟练的掌握并应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
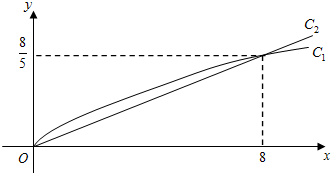
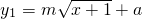 ,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.
,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.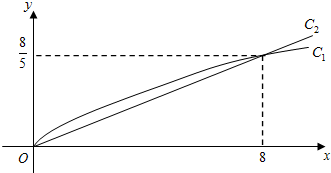
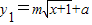 ,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.
,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.