题目内容
【题目】已知O为坐标原点，P为双曲线 
﹣y2=1（a＞0）上一点，过P作两条渐近线的平行线交点分别为A，B，若平行四边形OAPB的面积为 
，则双曲线的离心率为（ ）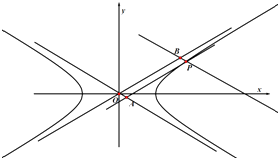
A.
B.
C.
D.
【答案】D
【解析】解：渐近线方程是：x±ay=0，设P（m，n）是双曲线上任一点，
过P平行于OA：x+ay=0的方程是：x+ay﹣m﹣an=0与OB方程：x﹣ay=0交点是B（ 
， 
），
|OB|=| | 
，P点到OB的距离是：d= 
∵平行四边形OAPB的面积为 
，
∴|OB|d=
∴| | = ，
即 
= 
，
∵ 
，∴ 
=1，
即m2﹣a2n2=a2 ， 代入得 
，
∴a= ，∴c=2，
∴e= 
= 
．
故选：D．
练习册系列答案
相关题目
【题目】下面有两个关于“袋子中装有红、白两种颜色的相同小球，从袋中无放回地取球”的游戏规则，这两个游戏规则公平吗？为什么？
游 戏 1 | 游 戏 2 |
2个红球和2个白球 | 3个红球和1个白球 |
取1个球，再取1个球 | 取1个球，再取1个球 |
取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
