Question

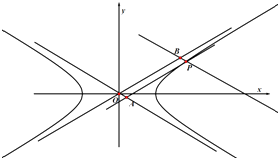
【题目】自平面上一点O引两条射线OA，OB，P在OA上运动，Q在OB上运动且保持| |为定值2 （P，Q不与O重合）．已知∠AOB=120°，
（I）PQ的中点M的轨迹是的一部分（不需写具体方程）；
（II）N是线段PQ上任﹣点，若|OM|=1，则 的取值范围是 ．

Answer 1

【答案】椭圆；[1﹣ ，1+ ]
【解析】解：（I）以OB为x轴，过O垂直于OB的直线为y轴，|OQ|=a，|OP|=b，则P（﹣ ， b），Q（a，0），
∴M（ ， b），
设M（x，y），则x= ，y= b，
∴a=2x+ y，b= y
由余弦定理可得a2+b2+ab=8，
∴3x2+4 xy+7y2=6，
∴PQ的中点M的轨迹是椭圆的一部分；
（II）∵| |为定值2 ，|OM|=1，
∴a2+b2=6，
∵a2+b2+ab=8，
∴ab=2，
∴a= ，b= ，
∴P（﹣ ， ），Q（ ，0），M（ ， ），
∴ =1﹣ ， =1+ ， =1
∴ 的取值范围是[1﹣ ，1+ ]．
所以答案是：椭圆；[1﹣ ，1+ ]．