题目内容
已知函数f(x)=
x3-
ax2+
(a>0)
(1)当a=3时,求f(x)的单调递增区间;
(II)求证:曲线y=f(x)总有斜率为a的切线;
(III)若存在x∈[-1,2],使f(x)<0成立,求a的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
| 9 |
| 2 |
(1)当a=3时,求f(x)的单调递增区间;
(II)求证:曲线y=f(x)总有斜率为a的切线;
(III)若存在x∈[-1,2],使f(x)<0成立,求a的取值范围.
(Ⅰ)当a=3时,
x3-
x2+
,
f′(x)=x2-3x,
令f′(x)=x2-3x>0解得x<0或x>3.
所以f(x)的单调递增区间(-∞,0),(3,+∞).
(II)f′(x)=x2-ax,
令f′(x)=x2-ax=a,即x2-ax-a=0,
因为a>0,
所以△=a2+4a>0恒成立,
所以方程x2-ax-a=0对任意正数a都有解,
所以曲线y=f(x)总有斜率为a的切线;
由(II)知,f′(x)=x2-ax,
令f′(x)=x2-ax=0得x1=0或x2=a,
因为a>0,所以当0<a<2时,x,f′(x),f(x)的变化情况如下表:
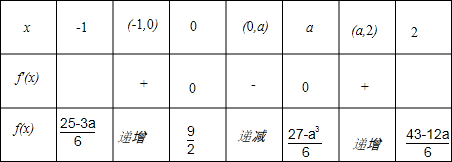
因为
>0,
>0,
所以,对应任意x∈[-1,2],f(x)>0,即此时不存在x∈[-1,2],使f(x)<0成立,
当a≥2时,x,f′(x),f(x)的变化情况如下表:
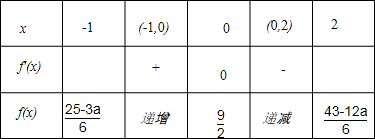
因为
-
=
≥0,
所以函数f(x)在[-1,2]上的最小值是
.
因为存在x∈[-1,2],使f(x)<0成立,
所以
<0,
所以a>
所以a 的取值范围为(
,+∞)
| 1 |
| 3 |
| 3 |
| 2 |
| 9 |
| 2 |
f′(x)=x2-3x,
令f′(x)=x2-3x>0解得x<0或x>3.
所以f(x)的单调递增区间(-∞,0),(3,+∞).
(II)f′(x)=x2-ax,
令f′(x)=x2-ax=a,即x2-ax-a=0,
因为a>0,
所以△=a2+4a>0恒成立,
所以方程x2-ax-a=0对任意正数a都有解,
所以曲线y=f(x)总有斜率为a的切线;
由(II)知,f′(x)=x2-ax,
令f′(x)=x2-ax=0得x1=0或x2=a,
因为a>0,所以当0<a<2时,x,f′(x),f(x)的变化情况如下表:

因为
| 25-3a |
| 6 |
| 27-a3 |
| 6 |
所以,对应任意x∈[-1,2],f(x)>0,即此时不存在x∈[-1,2],使f(x)<0成立,
当a≥2时,x,f′(x),f(x)的变化情况如下表:

因为
| 25-3a |
| 6 |
| 43-12a |
| 6 |
| 3a-6 |
| 2 |
所以函数f(x)在[-1,2]上的最小值是
| 43-12a |
| 6 |
因为存在x∈[-1,2],使f(x)<0成立,
所以
| 43-12a |
| 6 |
所以a>
| 43 |
| 12 |
所以a 的取值范围为(
| 43 |
| 12 |

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 则二项式
则二项式 的常数项是 .
的常数项是 . (用数字作答).
(用数字作答).