题目内容
 如图,已知点C的坐标是(2,2)过点C的直线CA与X轴交于点A,过点C且与直线CA垂直的直线CB与Y轴交于点B,设点M是线段AB的中点,则点M的轨迹方程为
如图,已知点C的坐标是(2,2)过点C的直线CA与X轴交于点A,过点C且与直线CA垂直的直线CB与Y轴交于点B,设点M是线段AB的中点,则点M的轨迹方程为x+y-2=0
x+y-2=0
.分析:由题意可知:点M既是Rt△ABC的斜边AB的中点,又是Rt△OAB的斜边AB的中点,可得|OM|=|CM|,利用两点间的距离公式即可得出.
解答:解:由题意可知:点M既是Rt△ABC的斜边AB的中点,又是Rt△OAB的斜边AB的中点.
∴|OM|=|CM|,
设M(x,y),则
=
,
化为x+y-2=0.
故答案为x+y-2=0.
∴|OM|=|CM|,
设M(x,y),则
| x2+y2 |
| (x-2)2+(y-2)2 |
化为x+y-2=0.
故答案为x+y-2=0.
点评:本题考查了直角三角形的斜边的中线的性质和两点间的距离公式,属于基础题.

练习册系列答案
相关题目
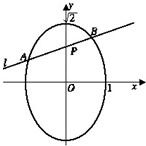 如图,已知椭圆C的方程为
如图,已知椭圆C的方程为 如图,已知圆C的圆心坐标为(1,-1),且过点M(2,-1).
如图,已知圆C的圆心坐标为(1,-1),且过点M(2,-1).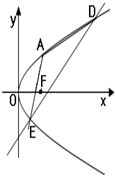 如图,已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.过A点作抛物线C的两条动弦AD、AE,且AD、AE的斜率满足kAD•kAE=2.
如图,已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.过A点作抛物线C的两条动弦AD、AE,且AD、AE的斜率满足kAD•kAE=2.