题目内容
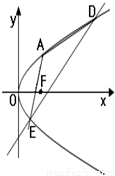
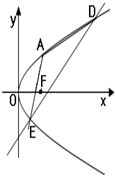 如图,已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.过A点作抛物线C的两条动弦AD、AE,且AD、AE的斜率满足kAD•kAE=2.
如图,已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.过A点作抛物线C的两条动弦AD、AE,且AD、AE的斜率满足kAD•kAE=2.(1)求抛物线C的方程;
(2)直线DE是否过某定点?若过某定点,请求出该点坐标;若不过某定点,请说明理由.
分析:(1)设抛物线方程为C:y2=2px(p>0),由抛物线定义及|AF|=2即可求得p值;
(2)设D(x1,y1),E(x2,y2),DE方程为x=my+n(m≠0),直线DE方程与抛物线方程联立消x得y的方程,由韦达定理及kAD•kAE=2可得关于m,n的关系式,从而直线DE方程可用m表示,由直线方程的点斜式即可求得定点.
(2)设D(x1,y1),E(x2,y2),DE方程为x=my+n(m≠0),直线DE方程与抛物线方程联立消x得y的方程,由韦达定理及kAD•kAE=2可得关于m,n的关系式,从而直线DE方程可用m表示,由直线方程的点斜式即可求得定点.
解答: 解:(1)设抛物线方程为C:y2=2px(p>0),
解:(1)设抛物线方程为C:y2=2px(p>0),
由其定义知|AF|=1+
,又|AF|=2,
所以p=2,y2=4x;
(2)易知A(1,2),设D(x1,y1),E(x2,y2),
DE方程为x=my+n(m≠0),
把DE方程代入C,并整理得y2-4my-4n=0,△=16(m2+n)>0,y1+y2=4m,y1y2=-4n,
由kAD•kAE=
•
=2及
=4x1,
=4x2,得y1y2+2(y1+y2)=4,即-4n+2×4m=4,
所以n=2m-1,代入DE方程得:x=my+2m-1,即(y+2)m=x+1,
故直线DE过定点(-1,-2).
 解:(1)设抛物线方程为C:y2=2px(p>0),
解:(1)设抛物线方程为C:y2=2px(p>0),由其定义知|AF|=1+
| p |
| 2 |
所以p=2,y2=4x;
(2)易知A(1,2),设D(x1,y1),E(x2,y2),
DE方程为x=my+n(m≠0),
把DE方程代入C,并整理得y2-4my-4n=0,△=16(m2+n)>0,y1+y2=4m,y1y2=-4n,
由kAD•kAE=
| y1-2 |
| x1-1 |
| y2-2 |
| x2-1 |
| y | 2 1 |
| y | 2 2 |
所以n=2m-1,代入DE方程得:x=my+2m-1,即(y+2)m=x+1,
故直线DE过定点(-1,-2).
点评:本题考查直线与圆锥曲线的位置关系及抛物线方程的求解,考查直线方程的点斜式,考查学生分析解决问题的能力.

练习册系列答案
相关题目
 (2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.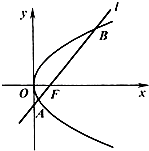 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.