题目内容
已知复数z满足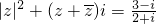 (i为虚数单位),求z.
(i为虚数单位),求z.
解:设z=x+yi,其中 x、y∈R,则由 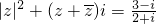 可得 x2+y2+2x•i=
可得 x2+y2+2x•i= ,
,
即 x2+y2+2xi= ,故有 x2+y2=1,2x=-1,
,故有 x2+y2=1,2x=-1,
解得 x=- ,y=±
,y=± ,故 z=-
,故 z=- ±
± .
.
分析:设z=x+yi,其中 x、y∈R,由题意可得 x2+y2+2xi= ,利用两个复数相等的充要条件求出x、y的值,即可求得z.
,利用两个复数相等的充要条件求出x、y的值,即可求得z.
点评:本题主要考查复数代数形式的混合运算,两个复数相等的充要条件,属于基础题.
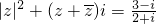 可得 x2+y2+2x•i=
可得 x2+y2+2x•i= ,
,即 x2+y2+2xi=
 ,故有 x2+y2=1,2x=-1,
,故有 x2+y2=1,2x=-1,解得 x=-
 ,y=±
,y=± ,故 z=-
,故 z=- ±
± .
.分析:设z=x+yi,其中 x、y∈R,由题意可得 x2+y2+2xi=
 ,利用两个复数相等的充要条件求出x、y的值,即可求得z.
,利用两个复数相等的充要条件求出x、y的值,即可求得z.点评:本题主要考查复数代数形式的混合运算,两个复数相等的充要条件,属于基础题.

练习册系列答案
相关题目
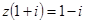 (i为虚数单位),则z等于
(i为虚数单位),则z等于 B.
B.
 C.
C. D.
D.
 (i为参数单位),则复数z的实部与虚部之和为 .
(i为参数单位),则复数z的实部与虚部之和为 . (i为参数单位),则复数z的实部与虚部之和为 .
(i为参数单位),则复数z的实部与虚部之和为 .