题目内容
“数学史与不等式选讲”模块
(1)用数学归纳法证明不等式:|sinnθ|≤n|sinθ|(n∈N*)
(2)求函数f(x)=sin3xcosx,x∈(0,
)的最大值.
(1)用数学归纳法证明不等式:|sinnθ|≤n|sinθ|(n∈N*)
(2)求函数f(x)=sin3xcosx,x∈(0,
| π | 2 |
分析:(1)先证明n=1时成立,计算n=k时,命题成立,利用放缩法,证明n=k+1时,命题成立;
(2)求导函数,取得函数的单调性,即可求得函数的最大值.
(2)求导函数,取得函数的单调性,即可求得函数的最大值.
解答:(1)证明:①n=1时,|sinθ|≤|sinθ|成立;
②假设n=k时,命题成立,即|sinkθ|≤k|sinθ|成立
则n=k+1时,|sin(k+1)θ|=|sinkθcosθ+sinθcoskθ|≤|sinkθ+sinθ|≤(k+1)|sinθ|
即n=k+1时,命题成立
综上,|sinnθ|≤n|sinθ|(n∈N*)
(2)解:求导函数可得f′(x)=sin2x(3cos2x-sin2x)
∵x∈(0,
),∴令f′(x)=0,可得x=
∵x∈(0,
),f′(x)>0,函数单调递增;x∈(
,
),f′(x)<0,函数单调递减
∴x=
时,函数取得最大值
.
②假设n=k时,命题成立,即|sinkθ|≤k|sinθ|成立
则n=k+1时,|sin(k+1)θ|=|sinkθcosθ+sinθcoskθ|≤|sinkθ+sinθ|≤(k+1)|sinθ|
即n=k+1时,命题成立
综上,|sinnθ|≤n|sinθ|(n∈N*)
(2)解:求导函数可得f′(x)=sin2x(3cos2x-sin2x)
∵x∈(0,
| π |
| 2 |
| π |
| 3 |
∵x∈(0,
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
∴x=
| π |
| 3 |
3
| ||
| 16 |
点评:本题考查数学归纳法,考查导数知识的运用,正确运用导数知识,掌握数学归纳法的证题步骤是关键.

练习册系列答案
相关题目
 为正实数,且
为正实数,且 .
. ;
; 的最小值.
的最小值.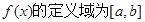 ,且
,且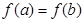 ,对于定义域内的任意实数
,对于定义域内的任意实数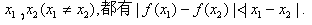 (1)设
(1)设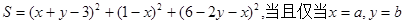 时,S取得最小值,求a,b的值;(2)在(1)的条件下,证明:对任意
时,S取得最小值,求a,b的值;(2)在(1)的条件下,证明:对任意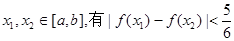 成立.
成立.