题目内容
数学自选模块
题号：03
“数学史与不等式选讲”模块（10分）
已知函数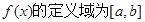
，且
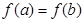，对于定义域内的任意实数
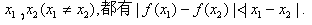（1）设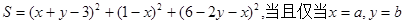
时，S取得最小值，求a，b的值；（2）在（1）的条件下，证明：对任意
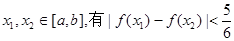成立.
【答案】
（1）解：由柯西不等式得
即
…………5分
（2）证明：不妨设
，
当
…………7分
当
故对任意
成立 …………10分
【解析】略
练习册系列答案
阅读快车系列答案
相关题目