题目内容
已知数列{an}的首项a1=3,通项an与前n项和Sn之间满足2an=Sn·Sn-1(n≥2).
(1)证明{![]() }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求数列{an}的通项公式.
(1)见解析
(2) an=Sn-Sn-1=![]() (n≥2).
(n≥2).
故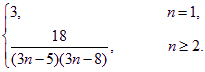
解析:
(1)当n≥2时,an=Sn-Sn-1,又2an=Sn·Sn-1,
∴2(Sn-Sn-1)=Sn·Sn-1.
两边同除以Sn·Sn-1得2(![]() -
-![]() )=1,
)=1,
即![]() -
-![]() =-
=-![]() .
.
∴{![]() }是等差数列,且首项
}是等差数列,且首项![]() =
=![]() =
=![]() ,公差为-
,公差为-![]() .
.
(2)由(1)知![]() =
=![]() +(n-1)×(-
+(n-1)×(-![]() )=
)=![]() ,
,
即Sn=![]() .
.
∴an=Sn-Sn-1=![]() (n≥2).
(n≥2).
故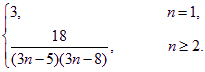

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目