题目内容
设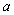 为实数,函数
为实数,函数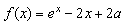 ,
,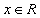 .
.
(I)求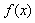 的单调区间与极值;
的单调区间与极值;
(II)求证:当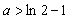 且
且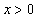 时,
时,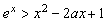 .
.
解:(1)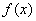 在
在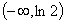 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
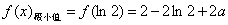 ,无极大值;
,无极大值;
(2)令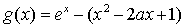 ,
,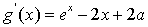 ,
,
由(1)知: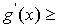
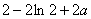 ,因为
,因为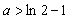 ,所以
,所以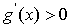 ,
,
所以 在
在 上单调递增,所以
上单调递增,所以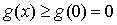 ,
,
即当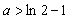 且
且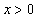 时,
时,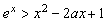

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
题目内容
设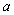 为实数,函数
为实数,函数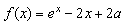 ,
,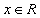 .
.
(I)求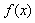 的单调区间与极值;
的单调区间与极值;
(II)求证:当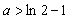 且
且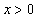 时,
时,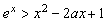 .
.
解:(1)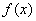 在
在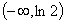 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
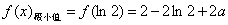 ,无极大值;
,无极大值;
(2)令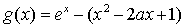 ,
,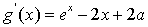 ,
,
由(1)知: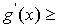
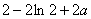 ,因为
,因为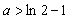 ,所以
,所以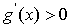 ,
,
所以 在
在 上单调递增,所以
上单调递增,所以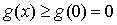 ,
,
即当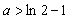 且
且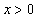 时,
时,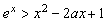

 智能训练练测考系列答案
智能训练练测考系列答案