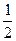题目内容
已知大西北某荒漠上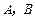 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以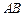 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
(1)试求四边形另两个顶点的轨迹方程;
(2)该荒漠上有一条直线型小溪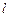 刚好通过点
刚好通过点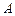 ,且
,且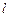 与
与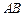 成
成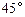 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
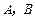 两点相距2千米,现准备在荒漠上围垦出一片以
两点相距2千米,现准备在荒漠上围垦出一片以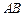 为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.
为一条对角线的平行四边形区域建农艺园.按照规划,围墙总长为8千米.(1)试求四边形另两个顶点的轨迹方程;
(2)该荒漠上有一条直线型小溪
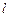 刚好通过点
刚好通过点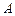 ,且
,且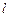 与
与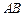 成
成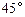 角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?
角.现要对整条小溪进行改造,因考虑到小溪可能被农艺园围进的部分今后重新设计改造,因此对该部分暂不改造.问暂不改造的部分有多长?(1)方程为 .(2)暂不改造的部分为
.(2)暂不改造的部分为 千米.
千米.
 .(2)暂不改造的部分为
.(2)暂不改造的部分为 千米.
千米.(1)设四边形的另两顶点为 ,则由题意,得
,则由题意,得 ,
, .
.
 ,
,
 点
点 的轨迹是以
的轨迹是以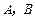 为焦点的椭圆.
为焦点的椭圆.
以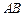 的中点为原点,
的中点为原点,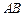 所在直线为
所在直线为 轴建立直角坐标系,
轴建立直角坐标系,
设 ,椭圆方程为
,椭圆方程为 ,
,
则 ,
,
 .
.
 方程为
方程为 .
.
(2)直线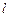 的方程为
的方程为 ,设
,设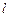 与椭圆相交于
与椭圆相交于 两点,且
两点,且 ,
,
由 得
得 ,
,
 ,
, .
.

 .
.
故暂不改造的部分为 千米.
千米.
 ,则由题意,得
,则由题意,得 ,
, .
. ,
, 点
点 的轨迹是以
的轨迹是以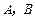 为焦点的椭圆.
为焦点的椭圆.以
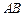 的中点为原点,
的中点为原点,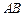 所在直线为
所在直线为 轴建立直角坐标系,
轴建立直角坐标系,设
 ,椭圆方程为
,椭圆方程为 ,
,则
 ,
, .
. 方程为
方程为 .
.(2)直线
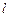 的方程为
的方程为 ,设
,设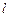 与椭圆相交于
与椭圆相交于 两点,且
两点,且 ,
,由
 得
得 ,
, ,
, .
.
 .
.故暂不改造的部分为
 千米.
千米.
练习册系列答案
相关题目
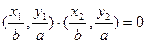 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.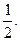 点
点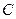 在
在 轴上,
轴上,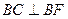 ,且
,且 、
、 三点确定的圆
三点确定的圆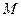 恰好与直线
恰好与直线 相切.
相切. 交椭圆于
交椭圆于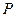 、
、 两点,在
两点,在 ,使得
,使得 恰好为△
恰好为△ 的内角平分线,若存在,求出点
的内角平分线,若存在,求出点
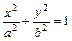 (a>b>0),动圆
(a>b>0),动圆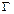 :
: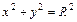 ,其中b<R<a. 若A是椭圆ε上的点,B是动圆
,其中b<R<a. 若A是椭圆ε上的点,B是动圆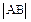 的最大值.
的最大值.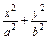 =1(a>b>0)上的三点,其中点
=1(a>b>0)上的三点,其中点 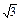 ,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.
,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|. 与
与 是否共线,并给出证明.
是否共线,并给出证明.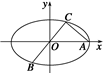
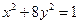 的焦点坐标是( ).
的焦点坐标是( ).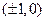
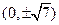
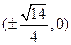
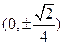
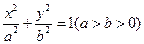 ,右焦点为
,右焦点为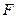 ,求连接
,求连接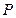 的线段
的线段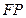 的中点
的中点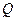 的轨迹方程.
的轨迹方程.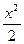 +
+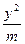 =1的离心率
=1的离心率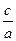 为
为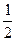 ,则m等于( )
,则m等于( )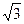
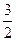
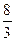
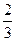
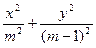 =1的准线平行于x轴,则m应满足的条件是( )
=1的准线平行于x轴,则m应满足的条件是( )