Question

（2012•黑龙江）设F₁、F₂是椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)的左、右焦点，P为直线x=

3a

2

上一点，△F₂PF₁是底角为30°的等腰三角形，则E的离心率为（　　）

• A．

  1

  2

• B．

  2

  3

• C．

  3

  4

• D．

  4

  5

Answer 1

分析：利用△F₂PF₁是底角为30°的等腰三角形，可得|PF₂|=|F₂F₁|，根据P为直线x=

3a

2

上一点，可建立方程，由此可求椭圆的离心率．

解答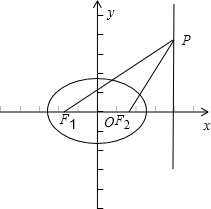：解：∵△F₂PF₁是底角为30°的等腰三角形，
∴|PF₂|=|F₂F₁|
∵P为直线x=

3a

2

上一点
∴2(

3

2

a-c)=2c
∴e=

c

a

=

3

4

故选C．

点评：本题考查椭圆的几何性质，解题的关键是确定几何量之间的关系，属于基础题