题目内容
已知|x-a|＜b的解集为{x|2＜x＜4}，则实数a等于（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：利用绝对值不等式的几何意义，去掉原不等式中的绝对值符号，得到a-b＜x＜a+b，依题意即可求得a的值．
解答：
解：∵|x-a|＜b，
∴a-b＜x＜a+b，
又|x-a|＜b的解集为{x|2＜x＜4}，
∴
，解得a=3．
故选：C．
∴a-b＜x＜a+b，
又|x-a|＜b的解集为{x|2＜x＜4}，
∴
|
故选：C．
点评：本题考查绝对值不等式的解法，着重考查等价转化思想与方程思想的应用，考查运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
算法流程图（如图所示）的运行结果为集合A={3，log2a}，B={a，b}，若A∩B={2}，则A∪B=（ ）
| A、{2，3，4} |
| B、{2，4} |
| C、{2，3} |
| D、{1，2，3，4} |
已知x与y成线性相关，其统计数据如下表：
则x与y的线性回归方程
=
x+
必过点（ ）
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
| A、（2，2） |
| B、（1.5，4） |
| C、（1.5，0） |
| D、（1，2） |
下列结论正确的是（ ）
①函数关系是一种确定性关系；
②在回归分析中，残差图中的纵坐标为残差；
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；
④复数-1+i的共轭复数是-1-i．
①函数关系是一种确定性关系；
②在回归分析中，残差图中的纵坐标为残差；
③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；
④复数-1+i的共轭复数是-1-i．
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
m∈R，复数（2m2-3m-2）+（m2-3m+2）i表示纯虚数的充要条件是（ ）
A、m=-
| ||
| B、m=2 | ||
C、m=-
| ||
| D、m=2或m=1 |
如图所示为一简谐振动的图象，则下列判断正确的是（ ）
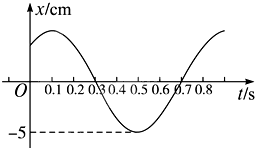
| A、该质点的振动周期为0.7s |
| B、该质点的振幅为5cm |
| C、该质点在0.1s和0.5s时振动速度最大 |
| D、该质点在0.3s和0.7s时的加速度为零 |
已知实数a，b满足a＞b，则下列说法一定正确的是（ ）
| A、a-c＞b-c | ||||
| B、a2＞b2 | ||||
C、
| ||||
| D、ac2＞bc2 |
若θ为锐角，求y=3cosθ•sin2θ的最大值是（ ）
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、1 |