题目内容
已知b>a,下列值:∫
f(x)dx,∫
|f(x)|dx,|∫
f(x)dx|的大小关系为( )
| ba |
| ba |
| ba |
A.|∫
| ||||||
B.∫
| ||||||
C.∫
| ||||||
D.∫
|
当函数y=f(x)在[a,b]上的图象在x轴上方,定积分就是求函数f(x)在区间[a,b]中图线下包围的面积,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积,此时∫
f(x)dx=∫
|f(x)|dx=|∫
f(x)dx|;
当函数y=f(x)在[a,b]上的图象在x轴下方,定积分就是求函数f(x)在区间[a,b]中图线上方包围的面积的负值,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积的负值,此时函数y=|f(x)|的图象在x轴上方,所以
|f(x)|dx=
f(x)dx|>0,
f(x)dx<0;
当函数y=f(x)的图象在[a,b]上x轴的上下方都有,不防设在[a,c)上在x轴上方,在(c,b]上在x轴下方,
则
f(x)dx为上方的面积减去下方的面积,|
f(x)dx|为上方的面积减去下方面积的绝对值,
|f(x)|dx为上方的面积加上下方的面积;
若函数y=f(x)的原函数为常数函数y=0,则∫
f(x)dx=∫
|f(x)|dx=|∫
f(x)dx|;
综上,三者的关系是
|f(x)|dx≥
f(x)dx|
f(x)dx.
故选B.
| ba |
| ba |
| ba |
当函数y=f(x)在[a,b]上的图象在x轴下方,定积分就是求函数f(x)在区间[a,b]中图线上方包围的面积的负值,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积的负值,此时函数y=|f(x)|的图象在x轴上方,所以
| ∫ | ba |
| |∫ | ba |
| ∫ | ba |
当函数y=f(x)的图象在[a,b]上x轴的上下方都有,不防设在[a,c)上在x轴上方,在(c,b]上在x轴下方,
则
| ∫ | ba |
| ∫ | ba |
| ∫ | ba |
若函数y=f(x)的原函数为常数函数y=0,则∫
| ba |
| ba |
| ba |
综上,三者的关系是
| ∫ | ba |
| |∫ | ba |
| ≥∫ | ba |
故选B.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
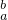 f(x)dx,∫
f(x)dx,∫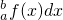 |的大小关系为
|的大小关系为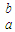 f(x)dx,∫
f(x)dx,∫ |f(x)|dx,|∫
|f(x)|dx,|∫ |的大小关系为( )
|的大小关系为( ) |≥∫
|≥∫ |f(x)|dx≥∫
|f(x)|dx≥∫ f(x)d
f(x)d |f(x)|dx≥|∫
|f(x)|dx≥|∫ f(x)dx|≥∫
f(x)dx|≥∫ f(x)d
f(x)d |f(x)|dx=|∫
|f(x)|dx=|∫ f(x)dx|=∫
f(x)dx|=∫ f(x)d
f(x)d |f(x)|dx=|∫
|f(x)|dx=|∫ f(x)dx|≥∫
f(x)dx|≥∫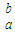 f(x)d
f(x)d