题目内容
已知b>a,下列值:∫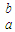 f(x)dx,∫
f(x)dx,∫ |f(x)|dx,|∫
|f(x)|dx,|∫ |的大小关系为( )
|的大小关系为( )A.|∫
 |≥∫
|≥∫ |f(x)|dx≥∫
|f(x)|dx≥∫ f(x)d
f(x)dB.∫
 |f(x)|dx≥|∫
|f(x)|dx≥|∫ f(x)dx|≥∫
f(x)dx|≥∫ f(x)d
f(x)dC.∫
 |f(x)|dx=|∫
|f(x)|dx=|∫ f(x)dx|=∫
f(x)dx|=∫ f(x)d
f(x)dD.∫
 |f(x)|dx=|∫
|f(x)|dx=|∫ f(x)dx|≥∫
f(x)dx|≥∫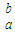 f(x)d
f(x)d
【答案】分析:根据定积分的几何意义,分别讨论函数y=f(x)及函数y=|f(x)|的图象在x轴上下方的可能情况,然后由微积分基本定理分析三个定积分对应曲边梯形的面积的大小.
解答:解:当函数y=f(x)在[a,b]上的图象在x轴上方,定积分就是求函数f(x)在区间[a,b]中图线下包围的面积,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积,此时∫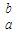 f(x)dx=∫
f(x)dx=∫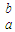 |f(x)|dx=|∫
|f(x)|dx=|∫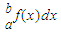 |;
|;
当函数y=f(x)在[a,b]上的图象在x轴下方,定积分就是求函数f(x)在区间[a,b]中图线上方包围的面积的负值,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积的负值,此时函数y=|f(x)|的图象在x轴上方,所以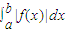 =
=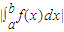 >0,
>0,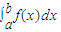 <0;
<0;
当函数y=f(x)的图象在[a,b]上x轴的上下方都有,不防设在[a,c)上在x轴上方,在(c,b]上在x轴下方,
则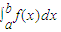 为上方的面积减去下方的面积,
为上方的面积减去下方的面积, 为上方的面积减去下方面积的绝对值,
为上方的面积减去下方面积的绝对值,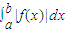 为上方的面积加上下方的面积;
为上方的面积加上下方的面积;
若函数y=f(x)的原函数为常数函数y=0,则∫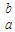 f(x)dx=∫
f(x)dx=∫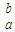 |f(x)|dx=|∫
|f(x)|dx=|∫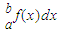 |;
|;
综上,三者的关系是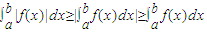 .
.
故选B.
点评:本题考查了不等关系与不等式,考查了利用微积分基本定理求定积分,解答此题的关键是对定积分的几何意义的理解与掌握,此题是中档题.
解答:解:当函数y=f(x)在[a,b]上的图象在x轴上方,定积分就是求函数f(x)在区间[a,b]中图线下包围的面积,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积,此时∫
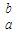 f(x)dx=∫
f(x)dx=∫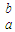 |f(x)|dx=|∫
|f(x)|dx=|∫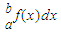 |;
|;当函数y=f(x)在[a,b]上的图象在x轴下方,定积分就是求函数f(x)在区间[a,b]中图线上方包围的面积的负值,即由 y=0,x=a,x=b,y=f(x)所围成图形的面积的负值,此时函数y=|f(x)|的图象在x轴上方,所以
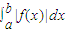 =
=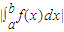 >0,
>0,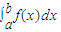 <0;
<0;当函数y=f(x)的图象在[a,b]上x轴的上下方都有,不防设在[a,c)上在x轴上方,在(c,b]上在x轴下方,
则
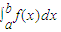 为上方的面积减去下方的面积,
为上方的面积减去下方的面积, 为上方的面积减去下方面积的绝对值,
为上方的面积减去下方面积的绝对值,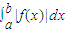 为上方的面积加上下方的面积;
为上方的面积加上下方的面积;若函数y=f(x)的原函数为常数函数y=0,则∫
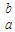 f(x)dx=∫
f(x)dx=∫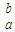 |f(x)|dx=|∫
|f(x)|dx=|∫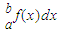 |;
|;综上,三者的关系是
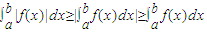 .
.故选B.
点评:本题考查了不等关系与不等式,考查了利用微积分基本定理求定积分,解答此题的关键是对定积分的几何意义的理解与掌握,此题是中档题.

练习册系列答案
相关题目
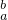 f(x)dx,∫
f(x)dx,∫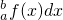 |的大小关系为
|的大小关系为