题目内容
已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示).
(I)求圆C的方程;
(II)若经过点(1,0)的直线l与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线l的方程.
(I)求圆C的方程;
(II)若经过点(1,0)的直线l与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线l的方程.
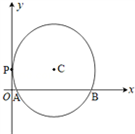
解:(I)因为圆C位于y轴右侧,且与y相切于点P(0,1),
所以圆心C在直线y=1上.又圆C被x轴分成的两段弧之比为1﹕2,
所以 .
.
所以PC=AC=BC=2,圆心C的坐标为(2,1).
所以所求圆C的方程为(x﹣2)2+(y﹣1)2=4.
(II)①若直线l斜率存在,设直线l的方程为y=k(x﹣1)(k≠0),
即kx﹣y﹣k=0.
因为线段EF为直径的圆恰好过圆心C,所以EC⊥FC.
因此 .
.
∵圆心C(2,1)到直线l的距离 .
.
∴由 得k=﹣1.
得k=﹣1.
故所求直线l的方程为y=﹣(x﹣1),即x+y﹣1=0.
②若直线l斜率不存在,此时直线l的方程为x=1,点E、F的坐标分别为 、
、 ,不满足条件.
,不满足条件.
故所求直线的方程为x+y﹣1=0.
所以圆心C在直线y=1上.又圆C被x轴分成的两段弧之比为1﹕2,
所以
 .
.所以PC=AC=BC=2,圆心C的坐标为(2,1).
所以所求圆C的方程为(x﹣2)2+(y﹣1)2=4.
(II)①若直线l斜率存在,设直线l的方程为y=k(x﹣1)(k≠0),
即kx﹣y﹣k=0.
因为线段EF为直径的圆恰好过圆心C,所以EC⊥FC.
因此
 .
.∵圆心C(2,1)到直线l的距离
 .
.∴由
 得k=﹣1.
得k=﹣1.故所求直线l的方程为y=﹣(x﹣1),即x+y﹣1=0.
②若直线l斜率不存在,此时直线l的方程为x=1,点E、F的坐标分别为
 、
、 ,不满足条件.
,不满足条件.故所求直线的方程为x+y﹣1=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知椭圆
已知椭圆 已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示).
已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示). 已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示).
已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示). 已知椭圆
已知椭圆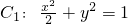 和圆
和圆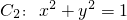 ,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.
,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.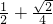 ,求证:AP⊥OP;
,求证:AP⊥OP;