题目内容
已知点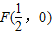 ,动圆P经过点F,与直线x=-
,动圆P经过点F,与直线x=- 相切,设动圆的圆心P的轨迹为曲线W,且直线x-y=m与曲线W相交于A(x1,y1),B(x2,y2)两点,O为坐标原点.
相切,设动圆的圆心P的轨迹为曲线W,且直线x-y=m与曲线W相交于A(x1,y1),B(x2,y2)两点,O为坐标原点.(1)求曲线W的方程;
(2)当m=2时,证明:OA⊥OB;
(3)当y1y2=-2m时,是否存在m∈R,使得
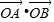 =-1?若存在,求出m的值;若不存在,请说明理由.
=-1?若存在,求出m的值;若不存在,请说明理由.
【答案】分析:(1)确定动圆圆心P的轨迹是以F为焦点,以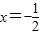 为准线的抛物线,即可得到曲线W的方程;
为准线的抛物线,即可得到曲线W的方程;
(2)直线方程与抛物线方程联立,求得A,B的坐标,即可得到结论;
(3)由于A,B两点在抛物线上,可得 ,利用
,利用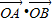 =-1,建立方程,即可求出m的值.
=-1,建立方程,即可求出m的值.
解答: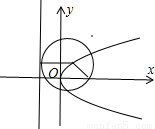 (1)解:过动圆圆心P作PN⊥直线
(1)解:过动圆圆心P作PN⊥直线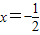 ,垂足为N,则有|PF|=|PN|,
,垂足为N,则有|PF|=|PN|,
∴动圆圆心P的轨迹是以F为焦点,以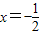 为准线的抛物线,
为准线的抛物线,
故曲线W的方程为y2=2x.
(2)证明:当m=2时,由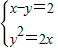 得x2-6x+4=0,
得x2-6x+4=0,
解得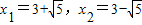 ,
,
因此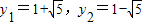 .
.
于是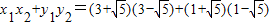 =0,
=0,
即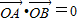 .
.
所以OA⊥OB
(3)解:假设存在实数m满足题意,由于A,B两点在抛物线上,故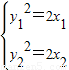
因此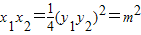 .
.
所以 .
.
由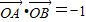 ,即m2-2m=-1,得m=1.
,即m2-2m=-1,得m=1.
又当m=1时,经验证直线与抛物线有两个交点,
所以存在实数m=1,使得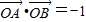 .
.
点评:本题考查轨迹方程,考查向量知识的运用,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.
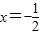 为准线的抛物线,即可得到曲线W的方程;
为准线的抛物线,即可得到曲线W的方程;(2)直线方程与抛物线方程联立,求得A,B的坐标,即可得到结论;
(3)由于A,B两点在抛物线上,可得
 ,利用
,利用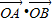 =-1,建立方程,即可求出m的值.
=-1,建立方程,即可求出m的值.解答:
 (1)解:过动圆圆心P作PN⊥直线
(1)解:过动圆圆心P作PN⊥直线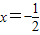 ,垂足为N,则有|PF|=|PN|,
,垂足为N,则有|PF|=|PN|,∴动圆圆心P的轨迹是以F为焦点,以
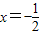 为准线的抛物线,
为准线的抛物线,故曲线W的方程为y2=2x.
(2)证明:当m=2时,由
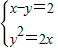 得x2-6x+4=0,
得x2-6x+4=0,解得
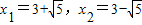 ,
,因此
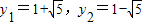 .
.于是
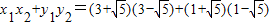 =0,
=0,即
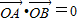 .
.所以OA⊥OB
(3)解:假设存在实数m满足题意,由于A,B两点在抛物线上,故
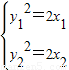
因此
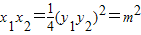 .
.所以
 .
.由
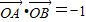 ,即m2-2m=-1,得m=1.
,即m2-2m=-1,得m=1.又当m=1时,经验证直线与抛物线有两个交点,
所以存在实数m=1,使得
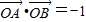 .
.点评:本题考查轨迹方程,考查向量知识的运用,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目