题目内容
已知各项均为正数的数列{an}的前n项和为Sn,首项为a1,且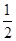 ,an,Sn成等差数列.
,an,Sn成等差数列.
(1)求数列{an}的通项公式;
(2)若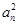 =
=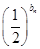 ,设cn=
,设cn=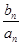 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
(1) an=2n-2 (2) Tn=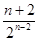
解析解:(1)由题意知2an=Sn+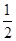 ,an>0,
,an>0,
当n=1时,2a1=a1+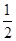 ,∴a1=
,∴a1=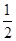 .
.
当n≥2时,Sn=2an-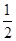 ,
,
Sn-1=2an-1-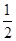 ,
,
两式相减得an=2an-2an-1,
整理得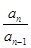 =2,
=2,
∴数列{an}是以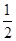 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
an=a1·2n-1=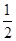 ×2n-1=2n-2.
×2n-1=2n-2.
(2)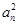 =
=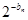 =22n-4,
=22n-4,
∴bn=4-2n,
∴cn=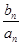 =
=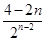 ,
,
即cn= .
.
则Tn=c1+c2+c3+…+cn,
即Tn=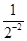 +
+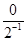 +
+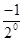 +…+
+…+ .
.
∴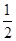 Tn=
Tn=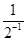 +
+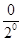 +
+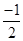 +…+
+…+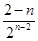 ,
,
则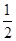 Tn=4+
Tn=4+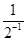 +
+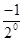 +…+
+…+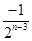 -
-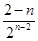 .
.
Tn=8-(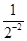 +
+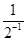 +…+
+…+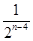 )+
)+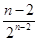
=8- +
+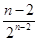
=8-8(1-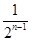 )+
)+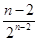
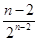
=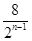 +
+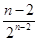
=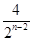 +
+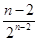 =
=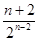 .
.
即Tn=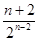 .
.

练习册系列答案
相关题目
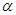 为锐角,且
为锐角,且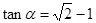 ,函数
,函数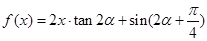 ,数列
,数列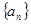 的首项
的首项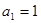 ,
, .
.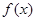 的表达式;(2)求数列
的表达式;(2)求数列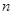 项和
项和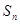 .
.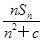 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数. 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.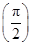 =0.
=0.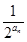 ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn.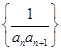 的前n项和,若Tn≤
的前n项和,若Tn≤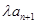 ¨对
¨对 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.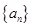 的首项为
的首项为 ,公差为
,公差为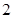 ,等比数列
,等比数列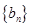 的首项为
的首项为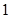 ,公比为
,公比为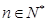 .
.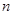 个正方形的边长为
个正方形的边长为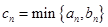 ,求前
,求前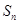 .
. 表示
表示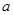 与
与 的最小值.)
的最小值.)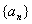 的首项
的首项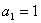 ,前
,前 项和为
项和为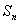 (
(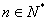 ),且点
),且点 在直线
在直线 上(
上(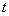 为与
为与 )为等比数列;
)为等比数列;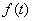 ,数列
,数列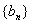 满足
满足 ,设
,设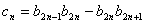 ,求数列
,求数列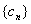 的前
的前 ;
;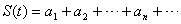 ,求函数
,求函数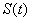 的值域.
的值域.