题目内容
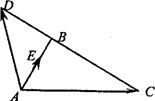如图，△ABC中，AB=4，AC=8，∠BAC=60°，延长CB到D，使BA=BD，当E点在线段AB上移动时，若| AE |
| AC |
| AD |
分析：由平面向量基本定理知，向量
一定可以由不共线的两向量
与
表示出来，即
=
+
=m
+n
（结合图形），所以m=
，n=
；又△ACD的形状是确定的，则|
|与|
|也是确定的，结合图形可知，当点E与点B重合时|
|、|
|相应地取得最大，即m、n取得最大值；此时把m、n用|DB|、|BC|、|DC|的比值形式表示出来，则m+n可求之．
| AE |
| AC |
| AD |
| AE |
| AM |
| AN |
| AC |
| AD |
| |AM| |
| |AC| |
| |AN| |
| |AD| |
| AC |
| AD |
| AM |
| AN |
解答：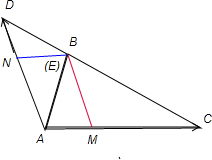
解：如图所示，作EM∥AD，EN∥AC．由题意知，当m取最大值时，点E与点B重合．
又∵
=
+
=m
+n
∴m=
=
，n=
=
．
∴m+n=
+
=1．
故答案为1．
解：如图所示，作EM∥AD，EN∥AC．由题意知，当m取最大值时，点E与点B重合．又∵
| AE |
| AM |
| AN |
| AC |
| AD |
∴m=
|
| ||
|
|
| |DB| |
| |DC| |
|
| ||
|
|
| |BC| |
| |DC| |
∴m+n=
| |DB| |
| |DC| |
| |BC| |
| |DC| |
故答案为1．
点评：对于向量的合成与分解问题，要充分利用图形并结合平行四边形法则（或三角形法则）来处理，往往会起到事半功倍的作用．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
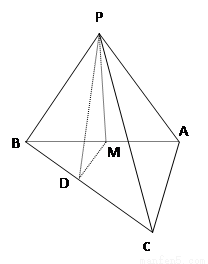
如图，△ABC中，∠A=90°，AB=4，AC=3，平面ABC外一点P在平面ABC内的射影是AB中点M，二面角P-AC-B的大小为45°．
如图在△ABC中，AB⊥AC，
