题目内容
已知椭圆 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 右焦点
右焦点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知 为椭圆
为椭圆 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.
解:(Ⅰ)由题意得 ,
,
由 可得
可得 ,
,
所以 ,
,
所以椭圆的方程为 .
.
(Ⅱ)由题意可得点 ,
,
所以由题意可设直线 ,
, .
.
设 ,
,
由 得
得 .
.
由题意可得 ,即
,即 且
且 .
.
 .
.
因为

 ,
,
所以直线 关于直线
关于直线 对称.
对称.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列为等差数列,,那么数列通项公式为( )
| A. | B. | ||
| C. | D. |
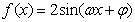
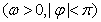 的部分图象如图所示,那么
的部分图象如图所示,那么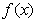 的表达式为
的表达式为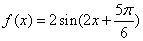 (B)
(B)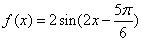
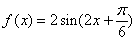 (D)
(D)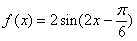

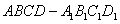 中,点
中,点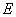 是棱
是棱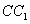 上的一个动点,平面
上的一个动点,平面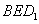 交棱
交棱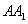 于点
于点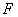 .则下列命题中假命题是 ( )
.则下列命题中假命题是 ( ) (A)存在点
(A)存在点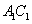 //平面
//平面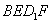
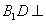 平面
平面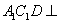 平面
平面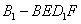 的体积均不变
的体积均不变 :
: 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 . 若点
. 若点 是椭圆
是椭圆 的最大值为
的最大值为 B.
B.  C.
C.  D.
D. 

 ,
, 满足约束条件
满足约束条件 则
则 的最大值为 .
的最大值为 .  中,点
中,点 ,
, ,若向量
,若向量 ,则实数
,则实数 _____.
_____. ( )
( ) B.
B. C.
C.  D.
D. 