题目内容

已知P是椭圆 $数学公式$ 上的动点，F₁，F₂是椭圆的两个焦点，则 $数学公式$ 的取值范围是________．

[-4，4]
分析：用坐标表示向量，求出数量积，根据椭圆的范围，即可确定 $\text{[math]}$ 的取值范围．
解答：设P的坐标为（x，y），则
∵椭圆 $\text{[math]}$ ，F₁，F₂是椭圆的两个焦点，∴F₁（-2 $\text{[math]}$ ，0），F₂（2 $\text{[math]}$ ，0）
∴ $\text{[math]}$ =（-2 $\text{[math]}$ -x，-y）•（2 $\text{[math]}$ -x，-y）=x²-8+y²= $\text{[math]}$ = $\text{[math]}$
∵0≤x²≤12
∴ $\text{[math]}$
∴ $\text{[math]}$ 的取值范围是[-4，4]
故答案为：[-4，4]
点评：本题考查向量的数量积，考查椭圆的标准方程，正确求出数量积是关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

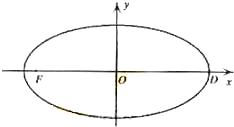已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为F(-

，0)，右顶点为D（2，0），设点A(1，

)．
（1）求该椭圆的标准方程；
（2）若P是椭圆上的动点，求线段PA中点M的轨迹方程；
（3）过原点O的直线交椭圆于点B，C，求△ABC面积的最大值．

已知F₁是椭圆

=1的左焦点，P是椭圆上的动点，A（1，1）是一定点，则PA+PF₁的最大值为

已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为F(-

，0)，右顶点为D（2，0），设点A(1，

)．
（Ⅰ）求该椭圆的标准方程；
（Ⅱ）若P是椭圆上的动点，求线段PA中点M的轨迹方程；
（Ⅲ）是否存在直线l，满足l过原点O并且交椭圆于点B、C，使得△ABC面积为1？如果存在，写出l的方程；如果不存在，请说明理由．

已知P是椭圆

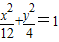上的动点，F₁，F₂是椭圆的两个焦点，则

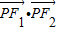的取值范围是．