题目内容
关于函数f(x)=4sin(2x- )(x∈R),有下列命题:
)(x∈R),有下列命题:(1)y=f(x+
 )为偶函数;
)为偶函数;(2)要得到函数g(x)=-4sin2x的图象,只需将f(x)的图象向右平移
 个单位;
个单位;(3)y=f(x)的图象关于直线x=-
 对称;
对称;(4)y=f(x)在[0,2π]内的增区间为[0,
 ]和[
]和[ ,2π];
,2π];(5)y=f(x)的周期为π.其中正确命题的序号是 .
【答案】分析:求出f(x+ )解析式,结合三角函数的奇偶性可得y=f(x+
)解析式,结合三角函数的奇偶性可得y=f(x+ )为非奇非偶函数,故(1)不正确;因为g(x)=f(x-
)为非奇非偶函数,故(1)不正确;因为g(x)=f(x- ),结合函数图象平移的规律可得(2)正确;当x=-
),结合函数图象平移的规律可得(2)正确;当x=- 时,f(-
时,f(- )=-4恰好是函数的最小值,所以y=f(x)的图象关于直线x=-
)=-4恰好是函数的最小值,所以y=f(x)的图象关于直线x=- 对称,故(3)正确;利用正弦函数单调区间的求法,可得y=f(x)在[0,2π]内的增区间为[0,
对称,故(3)正确;利用正弦函数单调区间的求法,可得y=f(x)在[0,2π]内的增区间为[0, ]和[
]和[ ,2π],故(4)正确;利用三角函数的周期公式可得(5)正确.
,2π],故(4)正确;利用三角函数的周期公式可得(5)正确.
解答:解:对于(1),∵f(x+ )=4sin[2(x+
)=4sin[2(x+ )-
)- ]=4sin(2x+
]=4sin(2x+ )
)
∴y=f(x+ )为非奇非偶函数,故(1)不正确;
)为非奇非偶函数,故(1)不正确;
对于(2),∵f(x)=4sin(2x- ),满足g(x)=f(x-
),满足g(x)=f(x- )=4sin[2(x-
)=4sin[2(x- )-
)- ]=-4sin2x
]=-4sin2x
∴将f(x)的图象向右平移 个单位,得到函数g(x)=-4sin2x的图象,故(2)正确;
个单位,得到函数g(x)=-4sin2x的图象,故(2)正确;
对于(3),当x=- 时,f(-
时,f(- )=4sin[2(-
)=4sin[2(- )-
)- ]=4sin(-
]=4sin(- )=-4,恰好是函数的最小值,
)=-4,恰好是函数的最小值,
∴y=f(x)的图象关于直线x=- 对称,故(3)正确;
对称,故(3)正确;
对于(4),令- +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,得-
+2kπ,得- +kπ≤x≤
+kπ≤x≤ +kπ,k∈z.
+kπ,k∈z.
取k=0和1,与区间[0,2π]取交集,得y=f(x)在[0,2π]内的增区间为[0, ]和[
]和[ ,2π],故(4)正确;
,2π],故(4)正确;
对于(5),y=f(x)的周期为 =π,故(5)正确.
=π,故(5)正确.
故答案为:(2)(3)(4)(5)
点评:本题以命题真假的判断为载体,考查了函数y=Asin(ωx+∅)的图象与性质,三角函数的周期性、单调性的奇偶性,属于中档题.
 )解析式,结合三角函数的奇偶性可得y=f(x+
)解析式,结合三角函数的奇偶性可得y=f(x+ )为非奇非偶函数,故(1)不正确;因为g(x)=f(x-
)为非奇非偶函数,故(1)不正确;因为g(x)=f(x- ),结合函数图象平移的规律可得(2)正确;当x=-
),结合函数图象平移的规律可得(2)正确;当x=- 时,f(-
时,f(- )=-4恰好是函数的最小值,所以y=f(x)的图象关于直线x=-
)=-4恰好是函数的最小值,所以y=f(x)的图象关于直线x=- 对称,故(3)正确;利用正弦函数单调区间的求法,可得y=f(x)在[0,2π]内的增区间为[0,
对称,故(3)正确;利用正弦函数单调区间的求法,可得y=f(x)在[0,2π]内的增区间为[0, ]和[
]和[ ,2π],故(4)正确;利用三角函数的周期公式可得(5)正确.
,2π],故(4)正确;利用三角函数的周期公式可得(5)正确.解答:解:对于(1),∵f(x+
 )=4sin[2(x+
)=4sin[2(x+ )-
)- ]=4sin(2x+
]=4sin(2x+ )
)∴y=f(x+
 )为非奇非偶函数,故(1)不正确;
)为非奇非偶函数,故(1)不正确;对于(2),∵f(x)=4sin(2x-
 ),满足g(x)=f(x-
),满足g(x)=f(x- )=4sin[2(x-
)=4sin[2(x- )-
)- ]=-4sin2x
]=-4sin2x∴将f(x)的图象向右平移
 个单位,得到函数g(x)=-4sin2x的图象,故(2)正确;
个单位,得到函数g(x)=-4sin2x的图象,故(2)正确;对于(3),当x=-
 时,f(-
时,f(- )=4sin[2(-
)=4sin[2(- )-
)- ]=4sin(-
]=4sin(- )=-4,恰好是函数的最小值,
)=-4,恰好是函数的最小值,∴y=f(x)的图象关于直线x=-
 对称,故(3)正确;
对称,故(3)正确;对于(4),令-
 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,得-
+2kπ,得- +kπ≤x≤
+kπ≤x≤ +kπ,k∈z.
+kπ,k∈z.取k=0和1,与区间[0,2π]取交集,得y=f(x)在[0,2π]内的增区间为[0,
 ]和[
]和[ ,2π],故(4)正确;
,2π],故(4)正确;对于(5),y=f(x)的周期为
 =π,故(5)正确.
=π,故(5)正确.故答案为:(2)(3)(4)(5)
点评:本题以命题真假的判断为载体,考查了函数y=Asin(ωx+∅)的图象与性质,三角函数的周期性、单调性的奇偶性,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 )(
)( ),有下列命题:
),有下列命题: 可得
可得 必是
必是 的整数倍;
的整数倍;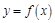 的表达式可改写为
的表达式可改写为 ;
; 对称;
对称; 对称.
对称.